月: 2024年3月

2024年習近平政権の動向　全人代総括リポート
https://www.nikkei.com/live/event/EVT240226002/live

中国恒大に罰金870億円　売上高11.7兆円の虚偽記載で
https://www.nikkei.com/article/DGXZQOGM18C4Z0Y4A310C2000000/

『【上海=土居倫之】経営再建中の中国不動産大手、中国恒大集団は18日、中国証券監督管理委員会から計5640億元（約11兆7000億円）の売上高の虚偽記載などで罰金約41億7500万元（約870億円）の処分を科されると発表した。創業者の許家印氏は終身にわたり、証券市場に関連する業務に就くことを禁じられる。

恒大の主要事業会社で社債の発行主体である恒大地産集団が18日発表した。発表によると、恒大は売上高を前倒しで計上するなどの方法で2019、20年決算に虚偽を記載した。

19年は当期の売上高の約50%に相当する2139億元、20年は同約78%に相当する3501億元をそれぞれ水増ししたという。これによって純利益も実態よりも大幅に多い金額を計上した。
こうした虚偽記載をもとに不正に社債を発行した疑いがあるという。

証券監督管理委員会は「恒大の各業務を全面管理し、業績の水増しを指示した」と許氏の責任を全面的に認めた。恒大には計41億7500万元、許氏には4700万元、夏海鈞・元最高経営責任者（CEO）には1500万元の罰金処分をそれぞれ科す。また許氏と夏氏には終身にわたり、上場・非上場企業の取締役や高級管理職に就くなど証券市場に関連する業務を禁じる。

恒大は23年、許氏が中国当局による拘束や逮捕を意味する「強制措置」を執られたと発表している。

中国の倪虹・住宅都市農村建設相は全国人民代表大会（全人代、国会に相当）期間中の記者会見で「重大な債務超過に陥り経営が困難となった企業は、破産すべきものは破産し、債務再編すべきものは再編すべきだ」と述べた。経営状態が深刻な不動産企業に今後厳しい対応を取る方針を示唆している。

【関連記事】

・法的整理の中国恒大、子会社2社は株取引再開
・恒大、中国当局は「延命」か　香港高裁が法的整理命令
・中国恒大、不採算の不動産事業を売却　60億円収益改善

多様な観点からニュースを考える

※掲載される投稿は投稿者個人の見解であり、日本経済新聞社の見解ではありません。

柯 隆のアバター
柯 隆
東京財団政策研究所　主席研究員
コメントメニュー

分析・考察

遅すぎるといわざるを得ない。証券監督当局はそれを見抜けなかったとすれば、それはそれで大問題である。見抜いてもっと早く処分しなかったのなら、なぜ？すでに債務超過が判明して、香港裁判所から破産命令を下された会社に、罰金を課すことを言い渡す唯一の意味は、大陸でも、恒大集団を政府が救済しないと決めたことであろう。
2024年3月19日 6:50　』

米国・イスラエル首脳、ラファ侵攻巡る高官協議で合意
https://www.nikkei.com/article/DGXZQOGN18CZ20Y4A310C2000000/

『2024年3月19日 5:27

【ワシントン=坂口幸裕】バイデン米大統領は18日、イスラエルのネタニヤフ首相と電話で話した。イスラエルが検討しているパレスチナ自治区ガザ最南部ラファでの地上侵攻を巡り、軍事計画や人道支援に関する高官協議を週内にも米国で開くと合意した。

米ホワイトハウスのサリバン大統領補佐官（国家安全保障担当）が18日の記者会見で明らかにした。週末から来週初めに予定する高官協議を実施するまでは「イスラエルが大規模な軍事作戦に踏み切ることはないだろう」との見方を示した。

サリバン氏は、バイデン氏がラファでの大規模な軍事作戦を「深く懸念している理由を説明した」と述べた。「軍事計画は統合された人道的、政治的な計画がなければ成功しない。ハマス打倒には持続可能な戦略が必要だ」と伝えたとも明言した。

両首脳が話すのは2月中旬以来になる。バイデン氏は民間人の保護を重視し、ラファ侵攻を「越えてはならない一線」とかねて警告。許容する条件として「市民の安全を確保する実行可能な計画」の提示を要求してきた。

ラファには避難民ら150万人が密集する。地上侵攻が始まれば、2023年10月のガザ戦闘開始から3万人超になった犠牲者の一段の拡大は避けられない。ネタニヤフ氏はハマス壊滅をめざし「ラファで軍事行動をとる。数週間かかるが実行する」と繰り返す。

サリバン氏は「ガザでの大規模な地上作戦は間違いだ。罪のない市民の死者を増やし、すでに悲惨な人道危機を悪化させ、イスラエルを国際的にさらに孤立させる」と強調した。
ラファへの地上侵攻を懸念する3つの理由をあげた。まずは民間人の安全や食料・住居を確保する計画を提示していないと指摘した。2つ目がガザへの人道支援の窓口となる場所で、物流機能が停止するリスクがあるためだ。

3つ目が国境を接するエジプトが慎重で、強行すれば今後の2国間関係が悪化しかねない点だ。サリバン氏は「イスラエルがラファで達成したい目標は他の手段でも達成できる」と提起。米首都ワシントンで開く軍事計画や人道支援に関する高官協議で打開策を探る。

米国内でアラブ系や若年層の間で犠牲者の増大を省みないイスラエルへの支援を堅持するバイデン氏への批判が広がる。11月に大統領選を控える同氏は神経をとがらせる。

米上院民主党トップのシューマー院内総務は14日、ネタニヤフ氏に早期に国会を解散して総選挙を実施するよう要求した。首相交代も視野に「イスラエル国民の大多数が変革の必要性を認識している」と唱えた。バイデン氏も演説内容を評価した。』

米EVのフィスカーが生産停止　破綻回避へ「大手と交渉」
https://www.nikkei.com/article/DGXZQOGN18CRO0Y4A310C2000000/

『2024年3月19日 4:55

【ニューヨーク=西邨紘子】経営危機に直面している米新興電気自動車（EV）のフィスカーは18日、6週間にわたり生産を停止すると発表した。資金繰りが悪化しており、在庫の拡大を防ぐ。同日に「大手自動車メーカーと提携交渉を進めている」とも表明し、経営破綻を回避するために注力していると訴えた。

フィスカーは18日、経営破綻を避けるための施策を公表した。そのうちの1つが一時的な生産停止で、在庫の拡大による資…

この記事は会員限定です。登録すると続きをお読みいただけます。』

日銀が大規模緩和解除へ、19日決定　長短金利操作も撤廃
https://www.nikkei.com/article/DGXZQOUB172JO0X10C24A3000000/

『2024年3月19日 2:00

【この記事のポイント】

・政策金利はマイナスから0〜0.1%へ転換
・長期金利の誘導目標撤廃、YCCは終了
・日本株ETFやREITの買い入れも廃止

日銀は19日の金融政策決定会合で大規模緩和の解除を決める方針だ。マイナス金利政策のほか、長期金利を抑え込むための長短金利操作（イールドカーブ・コントロール、YCC）や上場投資信託（ETF）などリスク資産を買い入れる枠組みもなくす。物価2%目標を持続的に達成…

この記事は有料会員限定です。登録すると続きをお読みいただけます。』

岐路に立つ米国株相場（平山賢一）
〈プロの羅針盤〉東京海上アセットマネジメント　参与　チーフストラテジスト
https://www.nikkei.com/article/DGXZQOUB047PD0U4A300C2000000/

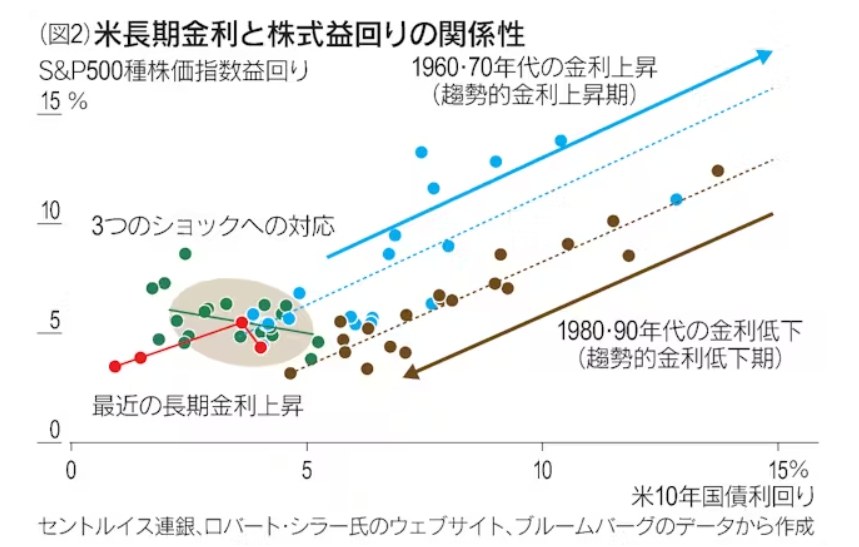
『2024年3月19日 4:00

日経平均株価が4万円を超えました。その背景の1つは米国株相場の上昇です。2020年3月の新型コロナ危機で急落した米株価指数は、22年の調整を乗り越えて高値を更新しました。インフレ率が低下し、早期の金融緩和への転換が期待される点が、米株式市場の参加者にとって支援材料であったようです。

そんな米株価指数の趨勢的な上昇が今後も期待できるか否かは、多くの人々にとって最大の関心事の一つになっています。特に…

この記事は会員限定です。登録すると続きをお読みいただけます。』

わりと身近なベイズ推定
https://note.com/hakuhodoproducts/n/n44fc5732fd26

　※　今日は、こんな所で…。

『2023年2月27日 17:00

自己紹介

初めまして。データビジネスデザイン事業本部の荒牧です。主に広告/施策の貢献量把握や、予算配分の最適化、未来予測など、データ分析周りを手広く行なっております。

今日はデータ分析を生業にしている方なら一度は耳にしたことがあるであろう「ベイズ推定(統計学)」についてお話ししたいと思います。
実はこれ、皆さんも日々知らず知らずのうちに活用しています。ベイズという言葉を初めて聞いたという方は、ぜひ一緒に考え方だけでも勉強してみましょう。

ベイズの定理とは

ベイズという名称はトーマス・ベイズという方の名前に由来しており、ベイズ推定の基となっているベイズの定理は以下の式で表されます。

画像

確率に関心がある方は理解できると思いますが、普段の生活では見かけない数式ですよね。

数式の理解が目的ではないので説明は割愛しますが、この理論は以下のような場面で活用されています。

迷惑メールのフィルタリング

ネットの検索エンジンの予測変換

ECサイトのレコメンド機能

こう言われると我々の身近に存在する理論だということがお分かりいただけるかと思います。

迷惑メールのフィルタリングとベイズ推定

迷惑メールのフィルタリング機能を例に、ベイズ推定の活用を考えてみましょう。

普段から受信しているアドレスからのメールであれば、迷惑メールか否かという判断は容易につきます。

しかしながら、初めて受信したアドレスからのメールについては、判断が難しいところです。そういったときに、メールの内容にURLが記載されているかどうかを判断材料として、ベイズ推定を試みてみます。

ベイズ推定とは「ある行動(情報)が得られた時に、状態Aである確率を、行動(情報)を基に考え直すこと」と考えてもらえれば良いと思います。

上記の例でいくと、メールの中にURLが入っているという「情報」が得られたときに、そのメールが迷惑メールである確率を算出し直すということです。

上記の例を用いてベイズ推定の流れをお話しすると、順序としては以下になります。

① 事前分布を設定。

② 行動(情報)が得られる。

③ 事後分布を推定し直す(算出し直す/考え直す）。

分布の説明に入ってしまうと、ややこしくなってしまいますので、割愛させてください(後ほど触れます)。

①はメールの内容を把握する前に、そのメールが迷惑メールだとフィルタリング機能が判断する確率、

②はメールの内容にURLが含まれていたという情報、

③は②の情報を考慮して、迷惑メールである確率を算出し直す、と考えることができます。※1

画像

普段受け取るメールに迷惑メールが多いからといって、全てを迷惑メール判定していたら大変なことになってしまいます。

ベイズ推定では、普段の傾向に、ある情報(ここではURLが入っているという情報)を得たことで、より正確に迷惑メールかどうかを判断する(確率を算出し直す)ことができるというわけです。

ベイズ推定は③の結果を①に置き直すことで、①→③の流れを繰り返すことができ、より現実的な確率に近付けていくことが可能です。

皆さんも日常生活において「何かしらの情報を基に改善していく」といった行動はきっと行なっています。それと同じです。

この推定方法は機械学習等、いろんな分析手法に絡めることができる理論であり、様々な場面で活用されています。実際に私も業務でこのベイズ推定を活用して、分析やモデリング等を行なっています。

一般的な統計的推定とベイズ推定の違い

ではこの理論を実務のどのような場面で使用しているのかですが

「回帰分析」や「ロジスティック回帰」といった言葉を耳にしたことはありませんか？

これらは膨大なデータから「要因となる数値」と「結果となる数値」の関係を調べ、それぞれの関係性を明らかにする分析手法です。

例えば、売上を上げている要因は何か、その要因はどれくらいの影響力があるのか、といったことを分析する際に使用できます。

上記の例において、要因 = 広告とすると、回帰分析では「広告の影響力は50です！」といった一意の値が結果となります。

ただ、上記を詳細に述べると「手元にある一部のデータから考えられる、広告の影響力は平均的に50です。」ということになります。

回帰分析自体は手軽に扱えて便利な分析手法ですが、こう言われると少し引っ掛かりますよね。

「一部のデータから」の部分について、ある程度のデータ量を確保できていれば大きな問題はありませんが、データ全体が見えていないにも関わらず、「影響力は50だ」と決めるのは、少し気になります。

この点に対し、ベイズ推定では「広告の影響力は50の可能性が高いが、49の可能性も少なからずあり、51の可能性もあるよね」といった考え方をします。

これが先ほど出てきた「分布」の正体です。（ベイズ推定の結果は一意の値ではなく、影響力の確率分布となります。）

画像

マーケティングの現場において利用される観測データには、調査誤差や観測誤差もあるでしょう。

より身近な例で考えると、飲酒量の平均が週あたり2缶という人でも、全く飲まない週もあれば、4缶以上飲む週もあると思います。

各データにバラ付きがあることを考慮した上で分析できるということは、現実に生きている生活者の行動を軸にしたモデリングと相性良く感じます。※2

上記分析においては、ある一時点(タイミング)の影響力の算出に留まっており、影響力は日々変わっていくことを考慮できておりませんが、構造時系列モデルといった状態空間モデルを取り入れることで、ベイズ推定を時系列データに対応させることもできます。

このように、分析手法は日々発展していきますが、それでも分析に限界はあります。

そのため、こういった分析/モデリングはこれまで「勘」や「経験」で向き合ってきた部分を代替えできるものではなく、勘や経験を軸に、新しい発見を見付けていくことが、マーケティングの中で数理モデルが果たす役割なのかと考えたりします。

ベイズ推定の良さは事前分布(情報/経験)を分析者側で設定できる部分にもあるので、そういった意味でも、今後も使われ続ける分析手法/推定法なのではないかと思います。

※1. 今回お話ししたベイズ推定の順序例③において「迷惑メールである確率を算出し直す」と記載していますが、詳細を述べると「迷惑メールであると判断する確率分布の期待値を、分布を推定し直すことで、算出し直す」となります。

※2. 一般的な統計的推定と比較して、ベイズ推定の方が良いというわけではなく、どちらにもメリット/デメリットがあります。そもそも無視できる誤差レベルであれば、誤差を考慮する必要はなく、回帰分析は非常に扱いやすい分析手法です。

※3. 条件付確率(とある条件下での確率)とベイズの定理は混同されやすいですが、条件付確率は時間の流れに沿って「Aが起こったときの結果Bの確率」を求めるものです。

ベイズの定理は条件付確率の逆確率であり、時間の流れに逆らって「結果Bを得たときのAの確率」を求めるものと考えられます。

※4. 事前情報(分布)を扱わないベイズ推定は最尤推定といいます。

#データ分析
#統計学
#確率分布
#ベイズ推定
#確率変数
#ベイズ確率
#BayesTheorem
#BayesianInference　』

現在の情報から過去を推定する（ベイズの定理）
https://note.com/kulamoto/n/n928b24814612

『HAYATA
5年間の金融関連業務を経て、 2022年より英大学院修士課程。専攻は金融リスク分析。

2022年12月13日 09:27

現在大学院で学んでいる分析についても細かく噛み砕いて記載していく。

他の学問も同じだが、分析について特に強く思うことは、「学んだこと＝使えること」とはならないこと。

例えば、このベイズの定理を学んだ時、「あっ、この分析手法はこのデータ（状況）に使えるかもしれない」という一種の閃きがすごく重要で、この閃きと頭の回転がなければ、いくら分析手法学んだとしても何のアウトプットも得られない（自分の力で分析できない）とすごく感じる。

だからこそ、この閃き力を養うために常に頭の中で日常生活を数値化し、その数値で遊んでみる、定理に当てはめてみるといったトレーニングが必要なのではないかと自分に言い聞かせる。

目次

ベイズの定理 (Bayes’ theorem)

ベイズの定理とは、
確率変数x, yについて成立する以下の公式を指す。

P(x=k|y=l) = P(y=l|x=k)×P(x=k) / P(y=l)

このP(x=k|y=l) は「『y=lである』という条件の時にx=kとなる確率」という条件付き確率を示している。

ベイズの定理の本質は、時間の向きを反転させること、つまり結果から原因に推定することにある。

抽象的な説明だと難しすぎるので、ここで、簡単な例を見てみる。
（以下、「本質を捉えたデータ分析のための分析モデル入門」杉山聡(2022)引用）

目の前に箱Aと箱Bがあります。箱Aの中には赤玉が３個、白玉が５個入っており、箱Bの中には赤玉が１個、白玉が３個入っています。あなたは無作為に箱A、Bのうちの一方を選び、その箱の中からランダムに１つ玉を取り出します。

この時、次の問題を解いてください。

(1)箱Aを選ぶ確率はいくらか？

(2)赤玉を取り出す確率はいくらか？

(3)箱Aを選び、かつ、赤玉を取り出す確率はいくつか？

(4)赤玉を取り出した時、実は選んだ箱が箱Aであった確率はいくつか？

まず、x,yをそれぞれ選んだ箱、玉の色に対応する確率変数としましょう。すると、この問題文では、

a) P(x=A) = P(x=B) = 1/2

b) P(y=赤|x=A) = 3/8

c) P(y=白|x=A) = 5/8

d) P(y=赤|x=B) = 1/4

e) P(y=白|x=B) = 3/4

であることがわかり、
これを用いると、すぐに計算することができます。

(1) aを用いて1/2

(2) (a×b) + (a×d) = 5/16

(3) a × b = 3/16

しかし、(4)は、与えられた確率の組み合わせに登場しません。
このような時に利用するのがベイズの定理です。

実際に条件を定理に当てはめると、
P(y=A|x=赤) = P(y=赤|x=A) × P(x=A) / P(y=赤)

この右辺に登場する確率は既に計算済みで、
P(y=A|x=赤) = (3/16) / (5/16) = 3/5

として、P(y=A|x=赤)も計算することができる。

ベイズの定理の計算式をみると、一見難しく見えるが、言葉で表すと単純で、

「箱Aを選び、かつ、赤玉を取り出す確率（(4)の順序を入れ替えたもの）」から、最後に「赤玉を取り出す確率」を割っただけになります。

この計算の何がすごいのか

そもそもなぜ(4)だけ素直に計算ができないのか。

その理由は、(1)から(3)は、この3つの条件付き確率は全て時間の流れと整合的な事象の確立を考えている問だからである。

また、問題文で与えられている確率は全て「どの箱を運ぶか」「箱を選んだ後どの玉を取り出すか」のように時間の流れと整合的なものばかりとなっている。

そのため、時間の流れに順行的な場合、原因→結果の自然な方向で考えればよく、素直に考えれば確率を計算できる。

一方、時間の流れに逆行する場合は、結果から原因を考えなければならない。

従って、他の問題と異なり計算が難しくなる。

この状況において、ベイズの定理は、本来は計算が非常に難しい時間逆行の条件付き確率を、簡単な時間順行の条件付き確率のみで表してくれる式なのだ。

また、基本的にデータ分析は結果から原因を推定する時間逆行の思考をするため、ベイズの定理やベイズ統計の考え方が使用されることが多い。

実例でみてみる

ベイズの定理を身近な事例で考えてみる。

事例：
病気の罹患率を調べる。

罹患率0.8%の病気について、罹患の有無を確認する検査を行う。

検査の精度は、
罹患者が陽性と診断される確率が95%、陰性と誤診断される確率が5%。
病気でない人（非罹患者）が陽性と誤診断される確率が20%、陰性と診断される確率が80%。

問：
検査の結果、陽性と診断された場合に本当に罹患している確率は？

時間の流れに沿った確率であれば、「病気に罹患する→検査を受けて陽性と診断」
として簡単に計算することができるが、時間と逆行した「検査を受けて陽性と判断→病気に罹患している」の確率を求める必要がある。

一旦、定理に当てはめると、

P(病気に罹患 | 陽性と診断) = P(陽性と診断 | 病気に罹患) × P(病気に罹患) / P(陽性と診断)

となり、
それぞれ計算すると、

P(陽性と診断 | 病気に罹患) = 0.95

P(病気に罹患) = 0.008

P(陽性と診断) = 罹患者が陽性と診断される確率 + 非罹患者が陽性と誤診断される確率
= (0.008×0.95) + (0.992×0.2)
= 0.206

P(病気に罹患|陽性と診断) = 0.95×0.008/0.206
= 0.0368932

よって、
検査の結果、陽性と診断された場合に本当に罹患している確率はたったの約3.69%しかないという結果になった。

この事例から分かることは、「一度の検査結果では本当に罹患しているかわからないので、再検査することが重要。」となる。

この事例は、適当に数字を入れて作ったよくある問題ではあるが、
コロナウイルスとPCR検査のデータを持ってきても同じように計算ができると考えてみると、
本当に身近なところでベイズの定理が活用されていることがわかる。

他にも、イギリス生活でよくある「スーパーで買ってきた食材が、中を開けるとカビが生えていた」場合の確率だとか色々とデータを考えることができる。』

ベイズの定理
https://ja.wikipedia.org/wiki/%E3%83%99%E3%82%A4%E3%82%BA%E3%81%AE%E5%AE%9A%E7%90%86

許容決定規則 ベイズ効率性 ベイズ確率 確率の解釈 ベイズの定理 ベイズ因子 ベイズ推定 ベイジアンネットワーク 事前確率 事後確率 尤度 共役事前分布 事後予測分布 ハイパーパラメータ ハイパーパラメータの事前分布 等確率の原理 最大エントロピー原理 経験ベイズ法 クロムウェルの差止め規則 ベルンシュテイン＝フォン・ミーゼス定理 シュワルツ情報量規準 信用区間 最大事後確率推定 根源的蓋然論

『出典: フリー百科事典『ウィキペディア（Wikipedia）』
統計学
ベイズ統計学
理論

技法

ベイズ線形回帰 ベイズ推定量 近似ベイズ計算 マルコフ連鎖モンテカルロ法

表話編歴

確率論

確率の公理

確率空間 標本空間 根元事象 事象 確率変数 確率測度

余事象 結合確立 周辺確率 条件付確率

独立 条件付き独立 全確率の法則 大数の法則 ベイズの定理 ブールの不等式

ベン図 樹形図

表話編歴

トーマス・ベイズ（c. 1701–1761）

確率論や統計学において、トーマス・ベイズ牧師にちなんで名付けられたベイズの定理（ベイズのていり、英: Bayes’ theorem）、ベイズの法則、最近ではベイズ・プライスの定理[1]とは、ある事象に関連する可能性のある条件についての事前の知識に基づいて、その事象の確率を記述するものである[2]。

例えば、健康問題の発生リスクが年齢とともに増加することが知られている場合、ベイズの定理により、ある年齢の個人のリスクを、単にその個人が集団全体の典型的な例であると仮定するよりも、（年齢を条件として）より正確に評価することができる。

ベイズの定理を応用したものに、推計統計学の手法の一つであるベイズ推定がある。

その際、定理に関わる確率は、異なる確率解釈をすることができる。

ベイズ確率の解釈では、定理は確率として表現された信念の度合いが、関連する証拠の入手可能性を考慮して合理的にどのように変化すべきかを表現している。ベイジアン推論は、ベイズ統計学の基本である。

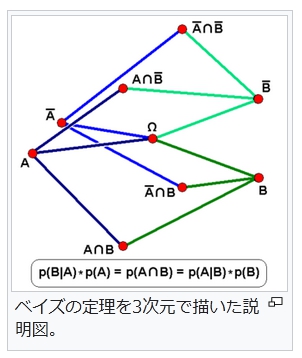
2つの樹形模様を重ね合せて表現したベイズの定理。

ベイズの定理を3次元で描いた説明図。

ピエール＝シモン・ラプラス（1745–1827）

定理の説明

ベイズの定理は数学的には次の式で表される[3]：

P ( A ∣ B ) = P ( B ∣ A ) P ( A ) P ( B ) {\displaystyle P(A\mid B)={\frac {P(B\mid A)\,P(A)}{P(B)}}}

ここで、 A {\displaystyle A} そして B {\displaystyle B} は事象であり、 P ( B ) ≠ 0 {\displaystyle P(B)\neq 0} である。

P ( A ∣ B ) {\displaystyle P(A\mid B)} は条件付き確率であり、 B {\displaystyle B} が真であるとき事象 A {\displaystyle A} が発生する確率である。

B {\displaystyle B} が与えられたときの A {\displaystyle A} の事後確率ともいう。
P ( B ∣ A ) {\displaystyle P(B\mid A)} もまた条件付き確率でもあり、 A {\displaystyle A} が 真である場合に B {\displaystyle B} が発生する確率である。

また、 P ( B ∣ A ) = L ( A ∣ B ) {\displaystyle P(B\mid A)=L(A\mid B)} であることから、固定された B {\displaystyle B} に対する A {\displaystyle A} の尤度とも解釈できる。

P ( A ) {\displaystyle P(A)} と P ( B ) {\displaystyle P(B)} は、与えられた条件なしに A {\displaystyle A} と B {\displaystyle B} がそれぞれ観測される確率で、周辺確率や事前確率と呼ばれている。

A {\displaystyle A}そして B {\displaystyle B}は別の事象である必要がある。

ベイズの定理の証明は P(A,B)=P(A|B)P(B)=P(B|A)P(A) から出る。

ベイズ推定
詳細は「ベイズ推定」を参照

ベイズの定理と組み合わせて確率的推論を行う方法がラプラスによって始められ、現在言うところのベイズ統計学の端緒となった。事象の確率という考え方を採用する特徴がある。

現在は例えば、迷惑メールの発見・分類といった作業のコンピュータを用いた自動化（フィルタリング）等のふるい分けにも利用されている。

概要

事象Bのベイズ確率について、

P(B) = 事象 A が起きる前の、事象 B の確率（事前確率, prior probability）

P(B|A) = 事象 A が起きた後での、事象 B の確率（事後確率，条件付き確率, posterior probability，conditional probability）

とする。 ベイズの定理を使えば、事後確率 P(B|A) は下記に従って計算される。

P ( B ∣ A ) = P ( A ∣ B ) P ( B ) P ( A ) {\displaystyle P(B\mid A)={\frac {P(A\mid B)\,P(B)}{P(A)}}}

すなわち、事象Aに関するある結果（データ）が得られたとすると、それを反映し、尤度 P(A|B) の乗算によって、事象 B の確率は事前確率から事後確率へと更新される。

なお事象 B の確率の観点からは、P(A) は規格化定数としての意味しかないため、しばしば省略される。つまり事後確率は事前確率と尤度の積に比例する：

P ( B ∣ A ) ∝ P ( A ∣ B ) P ( B ) = P ( A , B ) {\displaystyle P(B\mid A)\propto P(A\mid B)\,P(B)=P(A,B)}

ベイズ統計学（およびベイズ決定理論）は上記の手続きにその基礎をおき、名前の由来ともなっている[要出典]。

批判

ベイズ統計学では、事象の確率という考え方を採用し、必ずしも頻度には基づかない確率を「確率」として見なす。

またベイズの定理を用い、事前確率及び尤度を仮定した下で事後確率を与える、という相対的なメカニズムを主張している。

したがって事後確率の計算結果の信憑性や有用性は、事前分布と尤度の設定にかかっており、慎重を期すことが必要である。

これはベイズ統計学が、不確実性を含む問題を人によって異なる確率を用いて定式化することを許容する主観確率 (subjective probability) という立場をとっていることによる。

この立場はまだ解析対象となっていない新たな問題へのアプローチを可能にするという利点がある一方で、確率の決め方について客観性に欠けるという批判もある（客観確率）。
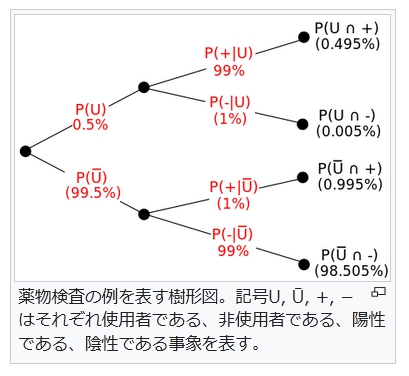
応用例

薬物検査

薬物検査の例を表す樹形図。記号U, Ū, +, − はそれぞれ使用者である、非使用者である、陽性である、陰性である事象を表す。

ある薬物の検査が感度99％かつ特異度99%だとしよう——つまり検査によって薬物の使用者のうち99%が陽性となり、非使用者のうち99%が陰性となると仮定する。

さらに社会の0.5%が薬物使用者であるとする。

無作為に選ばれた個人がこの検査で陽性だったとき、薬物使用者である確率はいくつか？ベイズの定理（と全確率の公式（英語版））から

P ( U ∣ + ) = P ( + ∣ U ) P ( U ) P ( + ) = P ( + ∣ U ) P ( U ) P ( + ∣ U ) P ( U ) + P ( + ∣ U ¯ ) P ( U ¯ ) = 0.99 × 0.005 0.99 × 0.005 + 0.01 × 0.995 ≈ 0.332 {\displaystyle {\begin{aligned}P({\text{U}}\mid {\text{+}})&={\frac {P({\text{+}}\mid {\text{U}})\,P({\text{U}})}{P(+)}}\\&={\frac {P({\text{+}}\mid {\text{U}})\,P({\text{U}})}{P({\text{+}}\mid {\text{U}})\,P({\text{U}})+P({\text{+}}\mid {\overline {\text{U}}})\,P({\overline {\text{U}}})}}\\&={\frac {0.99\times 0.005}{0.99\times 0.005+0.01\times 0.995}}\\&\approx 0.332\end{aligned}}}

個人の検査が陽性であるときでさえ、非使用者である可能性が使用者である可能性よりも高い。

（それでも検査結果が陽性であったという情報を反映して、事後確率 P ( U ∣ + ) ≈ 0.332 {\displaystyle P({\text{U}}\mid {\text{+}})\approx 0.332} は事前確率 P ( U ) = 0.005 {\displaystyle P({\text{U}})=0.005} よりも大幅に上昇している。）

つまり偽陽性の数は真陽性の数より多い。

これは非使用者が使用者に比べて多いからである。

たとえば、もし無作為に1000人が検査されるならば、995人の非使用者と5人の使用者がいると期待される。

995人の非使用者からは0.01 × 995 ≈ 10 人の偽陽性が期待される。

5人の使用者からは 0.99 × 5 ≈ 5人の真陽性が期待される。

よって陽性であると期待される15人のうち、5人のみが薬物使用者である。

この例における特異度の重要性が次の計算からわかる。

仮に感度が100%に上がり特異度が99%のままであれば陽性的中率は33.2%から33.4％に微増するに留まるが、感度が99%のままで特異度が99.5%に上がれば陽性的中率は49.9%に増加する。

脚注

^ Frame, Paul (2015). Liberty's Apostle. Wales: University of Wales Press. ISBN 978-1-78316-216-1 2021年2月23日閲覧。
^ Joyce, James (2003), Zalta, Edward N., ed., “Bayes' Theorem”, The Stanford Encyclopedia of Philosophy (Metaphysics Research Lab, Stanford University) 2020年1月17日閲覧。
^ Stuart, A.; Ord, K. (1994), Kendall's Advanced Theory of Statistics: Volume I—Distribution Theory, Edward Arnold, §8.7

参考文献

Bayes, Thomas; Price, Richard (1763). “An Essay towards solving a Problem in the Doctrine of Chance. By the late Rev. Mr. Bayes, communicated by Mr. Price, in a letter to John Canton, M. A. and F. R. S.” (PDF). Philosophical Transactions of the Royal Society of London (Royal Society) 53 (0): 370–418. doi:10.1098/rstl.1763.0053.
Gelman, Andrew; Carlin, John B.; Stern, Hal S.; Dunson, David B.; Vehtari, Aki; Rubin, Donald B. (2014). Bayesian Data Analysis. Texts in Statistical Science Series (Third ed.). CRC Press. ISBN 978-1-4398-4095-5. MR3235677. Zbl 1279.62004
Stigler, Stephen M. (1986). The History of Statistics. The Belknap Press of Harvard University Press. ISBN 0-674-40340-1. MR0852410. Zbl 0656.62005

関連項目

R言語
マルコフ連鎖モンテカルロ法
確率論
人工知能
全確率の法則（英語版）
単純ベイズ分類器
ベイジアンフィルタ
ベイズ確率
ベイジアン計量経済学
ベイズ推定
ベイズ統計学
ベイズ確率
ベイジアンネットワーク
推計統計学
確率分布
尤度関数
尤度比検定
最尤法
最大エントロピー原理
陽性尤度比
陰性尤度比
尤度方程式
条件付き確率
決定木

外部リンク

世界大百科事典 第2版『ベイズの定理』 - コトバンク
Weisstein, Eric W. "Bayes' Theorem". mathworld.wolfram.com (英語).

表話編歴

確率論
確率の歴史

アンドレイ・コルモゴロフ トーマス・ベイズ アンドレイ・マルコフ ジョゼフ・L・ドゥーブ 伊藤清

確率の定義
客観確率

統計的確率 古典的確率 公理的確率

主観確率

ベイズ確率

確率の拡張

外確率 負の確率

基礎概念
モデル

試行 結果 事象 標本空間 確率測度 確率空間

確率変数

確率変数の収束

確率分布

離散確率分布 連続確率分布 同時分布 周辺分布 条件付き確率分布 独立同分布

関数

確率質量関数 確率密度関数 累積分布関数 特性関数

用語

独立 期待値 モーメント 条件付き確率 条件付き期待値

確率の解釈

ベルトランの逆説 3囚人問題 モンティ・ホール問題 サンクトペテルブルクのパラドックス 合接の誤謬 ギャンブラーの誤謬

問題

壺問題 クーポンコレクター問題

法則・定理

ベイズの定理 大数の法則 中心極限定理 コルモゴロフの0-1法則 デ・フィネッティの定理 ウィーナー＝ヒンチンの定理

測度論

確率測度の拡張
    カラテオドリの拡張定理 E.ホップの拡張定理 コルモゴロフの拡張定理 ヴィタリの収束定理 優収束定理 ラプラス原理 スコロホッドの表現定理

確率微分方程式

伊藤の補題

確率過程

独立増分過程 定常過程 マルチンゲール マルコフ過程
    マルコフ性 マルコフ連鎖 マルコフ決定過程 部分観測マルコフ決定過程 マルコフ再生過程 ウィーナー過程
    ブラウン運動 幾何ブラウン運動 非整数ブラウン運動 ベルヌーイ過程 ガウス過程 自己相似過程 経験過程 中華料理店過程 オルンシュタイン＝ウーレンベック過程

情報量

最大エントロピー原理 交差エントロピー 結合エントロピー カルバック・ライブラー情報量 相互情報量

応用
数理ファイナンス

ブラック–ショールズ方程式 確率的ボラティリティモデル

系統学

ベイズ法

カテゴリ カテゴリ
典拠管理データベース: 国立図書館 ウィキデータを編集

ドイツ

カテゴリ:

確率論ベイズ統計トーマス・ベイズ数学のエポニム数学に関する記事

最終更新 2024年2月25日 (日) 13:25 （日時は個人設定で未設定ならばUTC）。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。

』