逆関数を求めることで何かメリットはあることはありますか?
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q14271968939
『逆関数を求めることで何かメリットはあることはありますか?
だいたい逆関数はただの計算問題しか出ないのでなんの目的でやるのかわかりません。出来れば高校の範囲で教えてください。あんまり計算以外で出題されないってことは大学の範囲だからかもしれないですけど…。』
『ベストアンサー
driさん
2022/12/4 15:13
◼️
逆関数は、もともとなんとなく理解している人ならば、習う前からすでにその考えを無意識に利用していると思います。
逆関数を習ったときに、「あ〜、あれって逆関数って名前なんだ」と気づく人もいれば、無意識に利用しているだけなので結びつかない人もいるでしょう。
◼️
習う前に利用していなかった人の場合は、その意味をすぐに理解するのは難しいかもしれません。
◼️
x| □ □ 2 6 8 □
y| -4 4 8 16 □ 28
例えばこんな表があって、数字は一次関数の値です。
そして、□の値を求めなさいという問題があったとします。
一次関数なので、
y=2x+4
ここまではすぐに分かりますね。
また、x=8のときは代入して、
y = 2×8+4 = 20
とすぐに出せます。
それにしても、xの方に□が3つもありますね。
1つならば、
28 = 2x+4
2x = 24
x = 12
このようにyに代入して計算しますね。
でも、たくさんあったら、もっと効率よくできないかと考えてみます。
y=2x+4
2x = y – 4
x = y/2 – 2
こうすれば、yの値を入れればxの値が計算できます。毎回移項が必要な計算をしなくてよくなります。
これは逆関数ではないように見えますが、
f(x) = 2x+4
として、
y = f(x)
x = f⁻¹(y)
こう書けば、f⁻¹はfの逆関数ですね。
逆関数は必ずしも、
y = f⁻¹(x)
という形である必要はありません。
fとf⁻¹という写像の関係性なのです。
◼️
また、逆関数の方が分かりやすい場合があります。
あるxと関数f(x)の値が、
( x , f(x) ) = (1 , 0) , (2 , 1) , (3 , 1.58496…) , …
これを見て、どんな関数かわからないとしても、逆関数の値を見ればすぐに分かります。
( x , f⁻¹(x) ) = (1 , 2) , (2 , 4) , (3 , 8) , …
これを見れば、
f⁻¹(x) = 2ˣ
で間違いないと考えられます。
よって、
f(x) = log₂x
だと分かります。
このように、逆関数の値を見た方が、元の関数を想像しやすい場合もあります。
実用的な面で言えば、このような考え方もよく使われると思います。
何事も、逆から考えたらよく分かったということはありますよね。
◼️
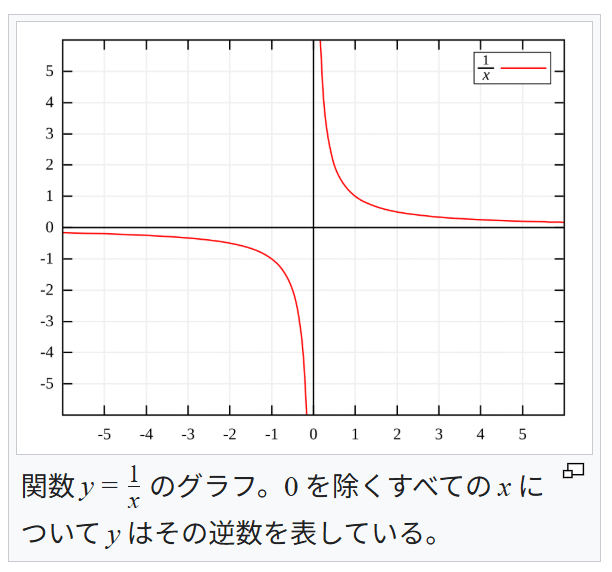
また、逆関数はy=xを対象軸として、グラフを線対称に反転したものになりますね。
上記y=2x+4のグラフは、y=xと(-4,-4)で交わります。
また、y=2x+4のグラフは切片(0,4)を通りますから、逆関数は(4,0)を通ることが分かります。
こう考えると、先ほどの問題のうち、2つの□は求められたことになります。
また、一次関数の逆関数は、傾きが逆数になるので、もう一つの□も、(28-4)/2=12だと暗算できます。
このように、逆関数の仕組みを知っていると、問題が楽に解ける場合があります。
ちょっと、例が単純すぎて参考にならないかもしれませんが。
◼️
あとは、微分での利用があります。
y=f(x)
とすると、
x=f⁻¹(y)
ですから、
y’ = (d/dx)f(x) = 1/{ (d/dy)f⁻¹(y) }
といった計算が可能です。
これも、逆関数で微分した方が圧倒的に簡単ならば、利用した方がよいという感じです。
高校数学の範囲では、高度な使い方になると思います。
◼️
以上かなと思います。
確かに計算問題以外では、使わなくても済むことがほとんどでしょう。
でも、知っていれば役立つときは、たまにあります。
頭の片隅には置いておくとよあのではないかと思います。』
『FuzzyGoriさん
2020/7/4 0:10
逆関数の意味が分からないのは、そもそも関数の意味が不明瞭だからです。
例えば、
引き算の意味は足し算から推測します。
それは逆関数も同様で、逆関数の意味は関数から推測します。
では、関数の意味とは何でしょうか?
実は、関数とは本質的に不明瞭なモノなのです。
どういう事かご説明する為、まず、足し算と関数の違いをご説明します。
そして次に、関数に意味を与える方法をご紹介します。
まず、
足し算とは、お金やリンゴなどを「加える」操作の抽象化です。
つまり、「何かを加える」というように、加える対象が不特定化されています。
ここで特筆すべき点は、足し算の意味が、加えるという「操作」によって定まっている点です。
一方、
関数とは、対象への「操作」の抽象化です。つまり、「対象に何かをする」というように、操作自体が不特定化されています。
ここでも加算と同様に、関数の意味は、「何かをする」という不明瞭な操作によって規定されます。
それゆえ、関数の意味は不明瞭になります。
よって、関数の意味を考察するには、足し算とは別の方法が必要なのです。
その方法とは、具体化する事です。
関数に具体的な意味を与えるには、具体的な関数を考えれば良いのです。
例えば、
足し算も一種の関数です。
なぜなら、関数=「対象に何かをする」の何かを「加える」に変えれば、足し算=「対象に加える」になります。
このとき、逆関数は引き算であり、逆関数の意味も明確に定まります。
もう1つ例を挙げると、
「受験生に受験番号を割当てる」という操作は、受験生を数へ対応付ける関数です。この関数の逆関数は、「番号から受験生を特定する」という操作です。
以下蛇足ですが、
先生が「意味が無い」と言ったのは決して間違いではありません。関数すべてに共通する意味は酷く抽象的で、無意味に等しいのですから。
一方、
現実的には、具体的な問題意識から具体的な関数が生み出されます。
ゆえに、「逆関数の意味は分からないが、とにかく求める必要がある」という状況は、学校の勉強だけの特殊な状況かと思います。』