NVIDIA製GPUの数十倍速い? 次々に出てくる「AI専用チップ」とは何者か 識者に聞く高速化の仕組み
https://www.itmedia.co.jp/aiplus/articles/2407/30/news137.html



『2024年07月31日 09時00分 公開
[斎藤健二,ITmedia]
印刷
見る
Share
57
2
スタートアップ企業の米Etchedが発表した「Sohu」が、AI業界に新たな波紋を投げかけている。トランスフォーマーモデルに特化したこのAI専用チップは、米NVIDIAのH100 GPUと比較して20倍高速かつ低コストで動作すると主張しているからだ。
SohuのようなAI専用チップの登場は、AI業界にどのような変革をもたらすのか。汎用性の高いGPUから特化型チップへの移行は、AI開発のアプローチをどう変えるのか。そして、こうした専用ハードウェアの普及は、ソフトウェア開発の方向性にどのような影響を与えるのか。
オーダーメイドによるAIソリューション「カスタムAI」の開発・提供を行うLaboro.AI(東京都中央区)の椎橋徹夫CEOに、AI専用チップがもたらす可能性と課題について聞いた。
Laboro.ai代表取締役CEOの椎橋徹夫氏
プロフィール:椎橋徹夫
米国州立テキサス大学理学部卒業後、ボストンコンサルティンググループに参画。消費財や流通など多数のプロジェクトに参画した後、社内のデジタル部門の立ち上げに従事。その後、東大発AI系のスタートアップ企業に創業4人目のメンバーとして参画。AI事業部の立ち上げをリード。東京大学工学系研究科松尾豊研究室にて「産学連携の取り組み」「データサイエンス領域の教育」「企業連携の仕組みづくり」に従事。同時に東大発AIスタートアップの創業に参画。2016年にLaboro.AIを創業し、代表取締役CEOに就任。
──現在のAIチップ市場はどのような状況でしょうか?
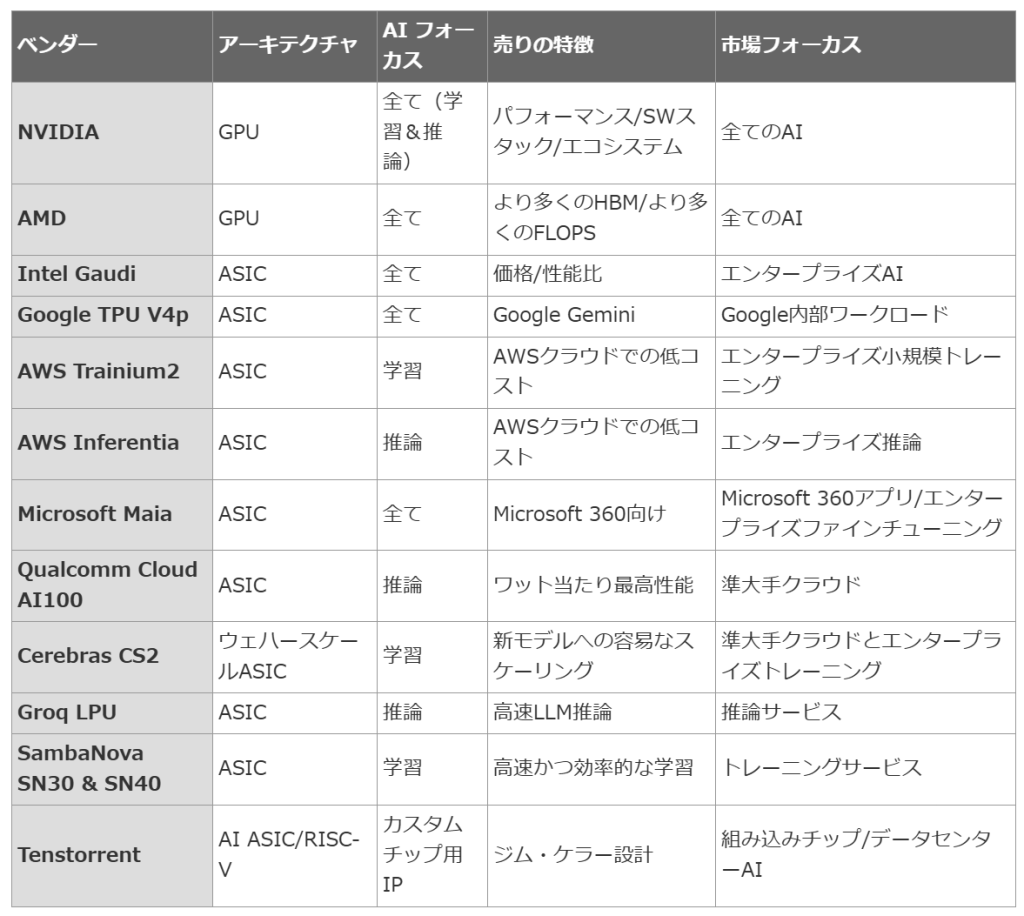
椎橋:現在のAIチップ市場には、大きく分けて2つの流れがあります。1つは汎用的なGPU(Graphics Processing Unit)で、もう1つは用途特化型のASIC(Application Specific Integrated Circuit:特定用途向け集積回路)です。
ベンダー アーキテクチャ AI フォーカス 売りの特徴 市場フォーカス
NVIDIA GPU 全て(学習&推論) パフォーマンス/SWスタック/エコシステム 全てのAI
AMD GPU 全て より多くのHBM/より多くのFLOPS 全てのAI
Intel Gaudi ASIC 全て 価格/性能比 エンタープライズAI
Google TPU V4p ASIC 全て Google Gemini Google内部ワークロード
AWS Trainium2 ASIC 学習 AWSクラウドでの低コスト エンタープライズ小規模トレーニング
AWS Inferentia ASIC 推論 AWSクラウドでの低コスト エンタープライズ推論
Microsoft Maia ASIC 全て Microsoft 360向け Microsoft 360アプリ/エンタープライズファインチューニング
Qualcomm Cloud AI100 ASIC 推論 ワット当たり最高性能 準大手クラウド
Cerebras CS2 ウェハースケールASIC 学習 新モデルへの容易なスケーリング 準大手クラウドとエンタープライズトレーニング
Groq LPU ASIC 推論 高速LLM推論 推論サービス
SambaNova SN30 & SN40 ASIC 学習 高速かつ効率的な学習 トレーニングサービス
Tenstorrent AI ASIC/RISC-V カスタムチップ用IP ジム・ケラー設計 組み込みチップ/データセンターAI
まず、GPUの方を見てみると、特にデータセンター向けのAIチップ市場では、NVIDIAのGPUが圧倒的なシェアを持っています。具体的には、90%以上のシェアを占めており、ほぼ独占状態と言っても過言ではありません。米AMDも一部GPUを作っていますが、NVIDIAの独占的な状況は変わりません。
一方で、ASIC、つまり用途特化型のチップの方では、いくつかの大手テクノロジー企業や新興企業が参入しています。例えば、米GoogleのTPU(Tensor Processing Unit)や、米AppleのNPU(Neural Processing Unit)などが挙げられます。これらは、それぞれの企業が自社の製品やサービスに最適化する形で開発しているASICです。
そして最近、特に注目を集めているのが、米Cerebras Systemsや米Groq、米Tenstorrentといったスタートアップ企業です。これらの企業は、AIの学習や推論に特化した新しいタイプのチップを開発しています。
──なぜこのような新興企業が出てきているのでしょうか?
椎橋:この背景には、AI全般に対する大規模な資金流入があります。AIの重要性が増す中で、AIの学習や推論に必要な計算資源に対するニーズが世界的に高まっています。それに伴い、より効率的な計算能力を提供するチップへの需要も急増しています。
また、NVIDIAのGPUの供給不足という状況も、新たなプレイヤーの参入を後押ししています。NVIDIAのGPUを製造している台TSMC(Taiwan Semiconductor Manufacturing Company)の生産能力がボトルネックとなり、GPUが不足する事態が起きています。この状況下で、新たなソリューションを提供する企業が注目を集めているわけです。
──新興企業の中でも特に注目されている企業はどこですか?
椎橋:特に注目を集めているのは、Cerebras Systems、Groq、そしてSohuを発表したEtchedです。加えて、つい先日ソフトバンクグループが買収を発表したGraphcore、理化学研究所も試験的に採用をしているSambaNova Systemsも有名です。
Etchedが発表したトランスフォーマー特化型チップ「Sohu」
Cerebras Systemsのウェハースケールエンジンは、従来のチップ製造方法を根本から変えようとする非常に野心的なアプローチです。
通常、半導体チップは、円形のシリコンウェハーから複数の小さなチップを切り出して作ります。これは生産効率を上げるための方法ですが、チップの大きさには制限があります。それに対してCerebrasは、ウェハー全体を1つの巨大なチップとして使用します。これにより、従来のNVIDIAのGPUと比較して、面積で50倍以上、搭載できるコア数で100倍以上、メモリ容量でギガバイトからテラバイトレベルへと大幅に増やすことができます。
このアプローチの利点は、チップ間の通信が不要になることです。従来の方式では、複数のチップ間でデータをやりとりする必要がありましたが、ウェハースケールエンジンではそれが不要になるため、処理速度と効率が大幅に向上します。
ただし、これほど大きなチップを製造することは技術的に非常に難しく、生産歩留まりの問題もあります。また、これだけ大規模なチップを冷却することも課題となります。
Groqは、元GoogleのTPU開発者が立ち上げた会社で、LPU(Language Processing Unit)と呼ばれる、大規模言語モデルの推論に特化したチップを開発しています。Ethcedは最近登場した企業で、トランスフォーマーに特化したチップを開発しています。
これらの企業は、従来のGPUとは異なるアプローチで、AIの処理を高速化・効率化しようとしている点で注目を集めています。
──GroqやEthcedのアプローチはどのようなものですか?
椎橋:Groqは、大規模言語モデルの推論処理に特化したチップを開発しています。彼らが開発しているLPUは、現在のAI、特に自然言語処理の分野で主流となっているトランスフォーマーアーキテクチャ等をベースとした言語モデルの特性に合わせて最適化されています。
実際の性能としては、例えば700億パラメータのモデルで1秒間に350トークンを生成できるほどの速度を達成しています。これは一般的なGPUと比較して非常に高速です。
一方、Sohuはさらに踏み込んで、トランスフォーマーアーキテクチャのみに特化したチップを開発しています。彼らのアプローチは、トランスフォーマーの処理特性に合わせてハードウェアを最適化するというものです。
そもそもトランスフォーマーはどのように動いているのか
──トランスフォーマーモデルの処理の特徴について、詳しく教えていただけますか?
椎橋:トランスフォーマーモデルの処理の特徴を理解するには、まず従来のRNN(Recurrent Neural Network)との違いを理解する必要があります。
RNNの処理の仕方は、入ってきた単語を順番にニューラルネットワークに入れて処理していきます。これまでに入力された単語の意味は、ニューラルネットワークの中に1つのベクトルとして圧縮されています。そして、新しく入ってきた単語との関係性だけを見ていくという形になります。つまり、これまで入ってきたものを「がっちゃんこ」した、総合としてのベクトルと、新しく入ってきた単語のベクトルの関係性を見るだけです。
一方、トランスフォーマーモデルは全く異なるアプローチを取ります。トランスフォーマーの核心部分は「アテンション機構」と呼ばれるもので、これが非常に特徴的です。
トランスフォーマーモデルでは、入力された全ての単語(トークン)同士の関係性を、それぞれ個別に計算します。例えば、10個の単語が入力されたとすると、1つの単語に対して他の9個の単語との関係性を全て見ていきます。そして、これを全ての単語に対して行います。
この処理方法により、文脈をより深く、より正確に理解できるようになります。直感的に考えても、全ての単語間の関係性を見る方が、より精度の高い理解ができそうだと想像できますよね。実際、この方法により、トランスフォーマーモデルは非常に高い性能を発揮しています。
ただし、この処理方法には大きなデメリットもあります。それは、計算量が膨大になるということです。入力されるトークンの数が増えれば増えるほど、計算量は飛躍的に増加していきます。
また、この処理には大量のメモリアクセスが必要になります。入力された文章をいったんメモリに置いて、そこから何度も参照しながら処理を行う必要があるからです。
さらに、この処理は並列化が難しいという特徴があります。全ての要素が互いに関係し合っているため、単純に処理を分割して並列に実行するということが難しいのです。
【トランスフォーマーの処理:分かりやすい例】
トランスフォーマーの処理、特にその核心であるアテンション機構を理解するために、次のような例を考えてみましょう。ある主(王様、政治家、組織長……)に仕える100人の専門家からなるアドバイザリーボードがいます。主は、アドバイザリーボードの意見(総意)を踏まえて、自らが信じる意思決定をします。
従来のRNNモデルでは、この状況を次のように処理します。
1人の人(仮にBさんとします)が立ち上がり、右隣のAさんに意見を聞きます。
Bさんは聞いた意見と自分の意見を合わせて要約し、左隣の次の人(Cさん)に渡します。
Cさんは、Bさんから受け取った要約と、自分の意見を合わせて新たな要約を作り、次の人に渡します。
これを100人全員が終わるまで繰り返します。
最後の100人目のアドバイザーは、主に要約を渡します
主はもともと持っていた自分の考えとアドバイザリーボードの総意(要約)を踏まえて意思決定をします
ここで問題なのは、次の2点です。
100人のアドバイザリーボードの要約は、最後に近いアドバイザーの意見ほど強く反映されがち(初めの方の人たちの意見は忘れられがち)
アドバイザリーボードは、主がもともと持っている考えを知らず、それを踏まえた意見集約にはなっていない
一方、トランスフォーマーモデルは、この状況を全く異なる方法で処理します。
全員が同時に立ち上がります
各人が、他の99人全員と直接会話を交わします
各人は、他の99人が自分の意見にとって有用な専門知見をどれだけを持っているかを見極めて、有用度に応じてそれぞれの意見を取り入れ自分の意見をアップデートします(アテンション)
これを全員が同時に行います
最後に、主が100人それぞれと会話をします
主は、もともとの自分の考えと各アドバイザーの意見の関連度合いを見極めて、関連度に応じて意見を取り入れて、最終的な意思決定をします。
このトランスフォーマーの方法には、いくつかの重要な特徴があります。
並列処理:全員が同時に情報交換を行うため、処理が高速です。
直接的な関係性の把握:各人が他の全員と直接対話するため、情報のひずみが少なくなります。
大量の計算:100人それぞれが99人と対話するため、総計9900回の対話が発生します。これは膨大な計算量を意味します。
メモリ要求:各人は99人分の情報を一時的に記憶する必要があります。これは大量のメモリを必要とすることを意味します。
この例で分かるように、トランスフォーマーモデルは非常に詳細で包括的な情報処理を行いますが、それには大量の計算リソースとメモリが必要になります。これが、トランスフォーマーモデルに最適化された特殊なハードウェアが必要とされる理由です。
──トランスフォーマーの特徴は、ハードウェア設計にどのような影響を与えるのでしょうか?
椎橋:トランスフォーマーモデルの特性は、従来のGPUで効率的に処理するのが難しい面があります。
トランスフォーマーの処理はRNNと比較するとGPUの計算に向いているものの、先ほど説明したように複雑に絡み合っているため、単純な並列計算に持ち込むのが難しいのです。
また、GPUとメモリの間でデータをやりとりする回数が多くなります。トランスフォーマーモデルの処理では、入力されたデータをメモリに置いて、それを何度も参照しながら計算を行います。そのため、メモリアクセスと演算処理の切り替えが頻繁に発生します。これは処理効率を下げる要因になります。
このような特性に対応するため、トランスフォーマーモデルに最適化されたハードウェア設計が重要になってきています。
その鍵となる基本的な考え方は、ハードウェア(チップ)が実行できる計算処理(命令セット)をそのモデルアーキテクチャの処理に必要な種類の計算に絞って、それぞれの種類の計算をする処理ユニットをちょうど良いバランスでそろえて配置することです。
手工業に例えるならば、CPUはどんな作業でもこなせる多能工が1人でいろいろな製品を作っている状態、GPUはどんな作業でもこなせる多能工が複数人で並行していろいろなパーツを作り組み立てている状態です。作りたい製品が多様な場合は効果的な方法ですが、作りたい製品と組み立てのプロセスが決まっている場合、これは非効率なやり方です。
ではどうしたらいいか。それは、必要な各作業に特化した単能工をそれぞれちょうど良い人数をそろえて、作業分担をする形で配置し、流れ作業のラインを作ることです。
先ほど述べたGroqのLPUは、その仕組みに「Tensor Streaming Processor」、つまり言語モデルの処理の中心になる行列(テンソル)のいくつかの種類の計算をユニット化して、ユニット間で処理データを受け渡していく流れ作業(ストリーミング)にする、という考え方を採用することで、言語モデルの推論の大幅な高速化を実現しています。
Groqチップのアーキテクチャ。やりたいことを言語モデルの処理に絞れば、「Matrix Unit=密行列の掛け算をする部分」「switch unit=データを流す処理の部分」「メモリ」「Vector Unit=ベクトルの計算を扱う部分」のようにシンプルな処理ユニットの種類を作って並べることができる
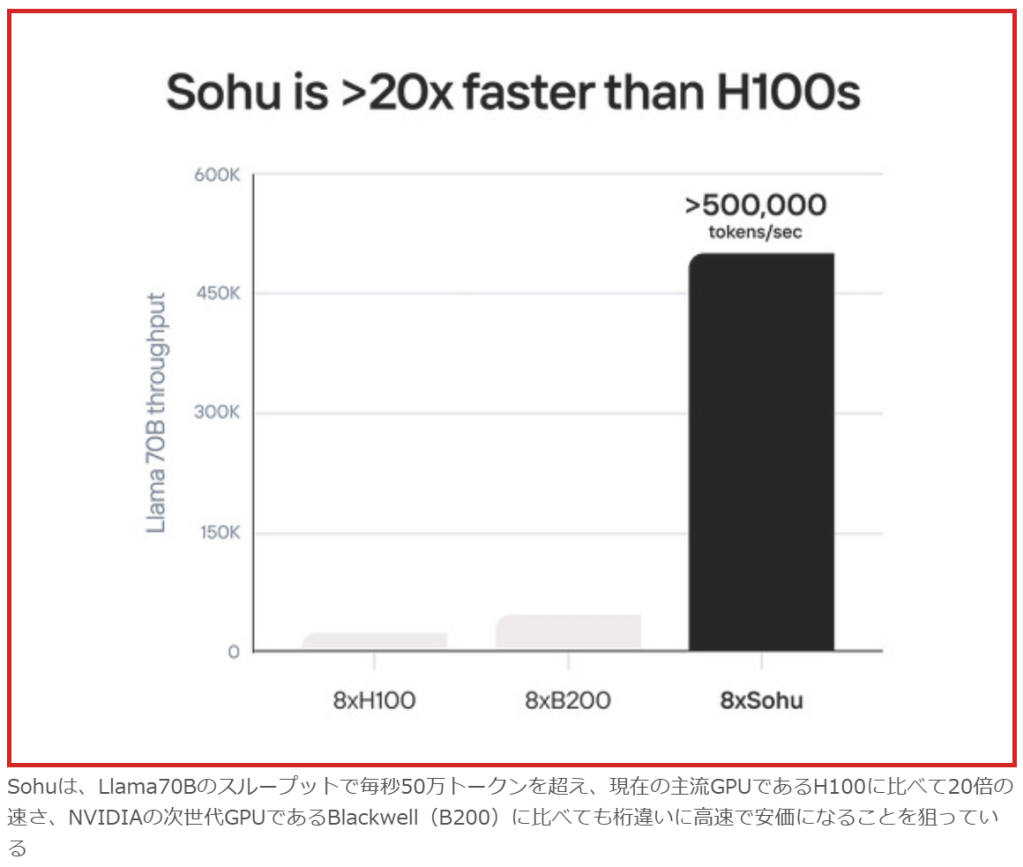
また、大胆にトランスフォーマーアーキテクチャのみに照準を定めるEtchedのSohuは、さらに細かくトランスフォーマーの計算処理プロセスにピッタリ合わせた計算ユニットの設計と配置を行いました。トランスフォーマーの処理であれば、従来GPUが計算リソースの30%程度しか有効に稼働させられていなかったところを、90%以上の稼働を実現しているとうたっています。
Sohuは、Llama70Bのスループットで毎秒50万トークンを超え、現在の主流GPUであるH100に比べて20倍の速さ、NVIDIAの次世代GPUであるBlackwell(B200)に比べても桁違いに高速で安価になることを狙っている
──トランスフォーマーモデルに特化したハードウェアには課題はありませんか?
椎橋:最大の課題は汎用性の低さです。トランスフォーマーモデルに最適化されたハードウェアは、他タイプのAIモデルをそもそも実行できなかったり、実行できても効率が大きく低下する可能性があります。
また、AIのアーキテクチャは急速に進化しています。例えば、最近では米MicrosoftのRetentive Networkや、画像処理分野でのMamba(選択的状態空間モデル)など、トランスフォーマー以外の新しいアーキテクチャも登場しています。特定のアーキテクチャに過度に最適化されたハードウェアは、新しいモデルが登場した際に陳腐化するリスクがあります。さらに、トランスフォーマーモデル自体も進化を続けています。ハードウェアの開発サイクルはソフトウェアよりも長いため、最新のモデルの特性に常に対応し続けることは難しい課題です。
ただ、こういった課題がある一方で、可能性もあります。トランスフォーマー向けASICがある程度普及すると、ハードウェアも含めて考えた場合、中期的にはトランスフォーマーモデルの方が有利な状況が続くかもしれません。
なぜかというと、現在のトランスフォーマーアーキテクチャは、特に大規模言語モデルの分野でほぼ独占状態にあるからです。そこにトランスフォーマー向けASICが普及すると、ソフトウェアの効率だけで見れば優れた新モデルが登場しても、ハードウェアも含めて考えるとトランスフォーマーの方が全体的に性能が良いという状況が生まれるかもしれないからです。この相互作用が、トランスフォーマーモデルの優位性をさらに強化する可能性があるのです。
AIチップで垂直統合のアプローチが増える?
これまでのコンピュータ産業、特にソフトウェア産業は、水平分業によって急速な発展を遂げてきた。ハードウェアとソフトウェアを分離することで、それぞれの分野で専門性を高め、イノベーションを加速させてきたのである。しかし、AIの世界では状況が少し異なるようだ。大規模な言語モデルの学習や推論には膨大な演算能力が必要で、エネルギー効率も重要な課題となっている。このリソースの制約に対処するためには、ハードウェアとソフトウェアを緊密に連携させる必要があるからだ。
そのため、AIチップの開発では、従来の水平分業よりも、ソフトウェアとハードウェアをすり合わせた垂直統合型のアプローチが増えていく可能性がある。これは、製造業における「すり合わせ」の文化を持つ日本にとって、新たな機会となるかもしれない。自動車産業や産業用ロボットなど、日本が強みを持つ分野でのAI応用と組み合わせることで、日本の半導体産業が再び世界で競争力を持つ可能性もあるだろう。
』