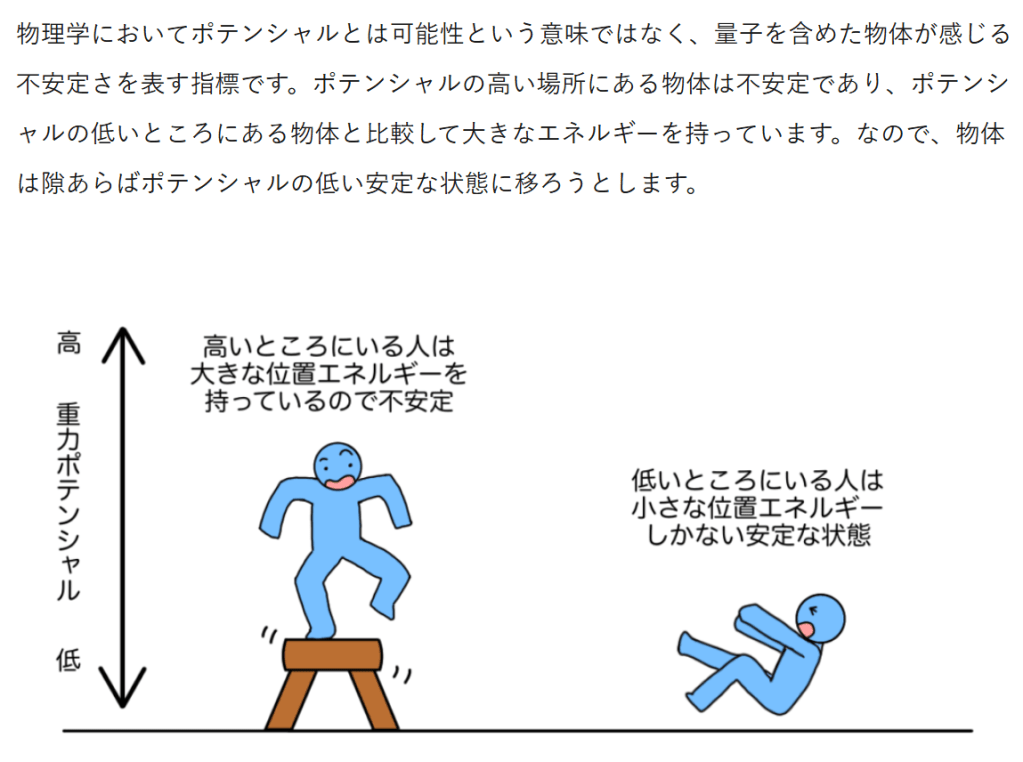
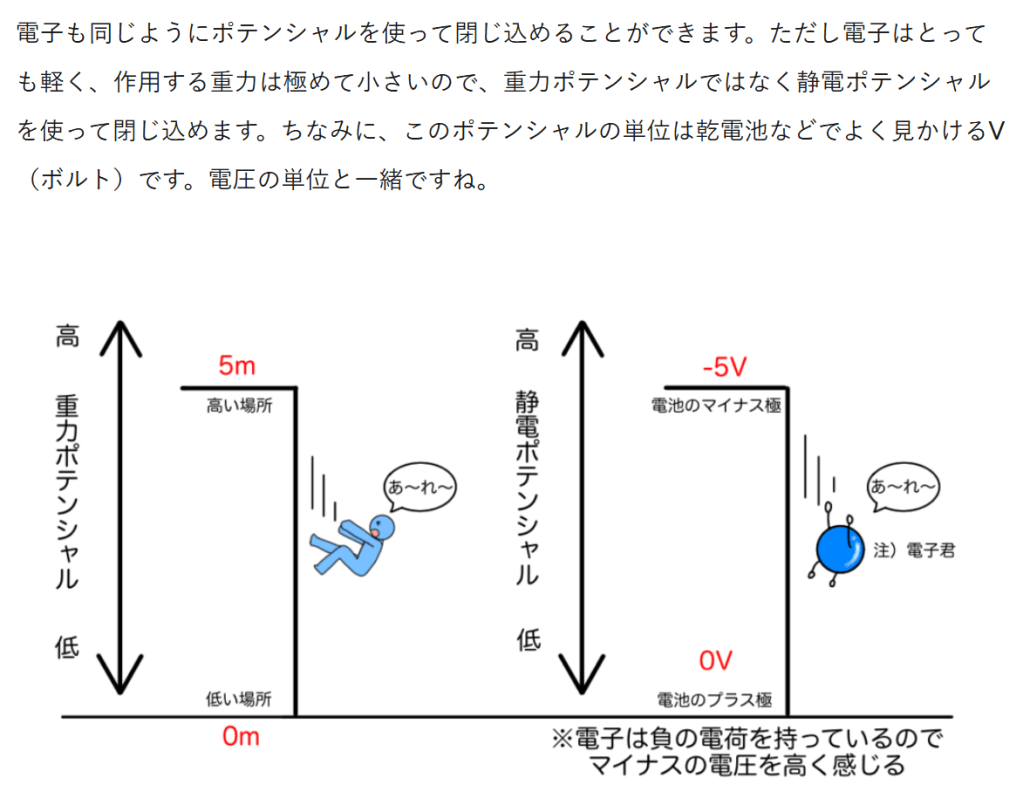
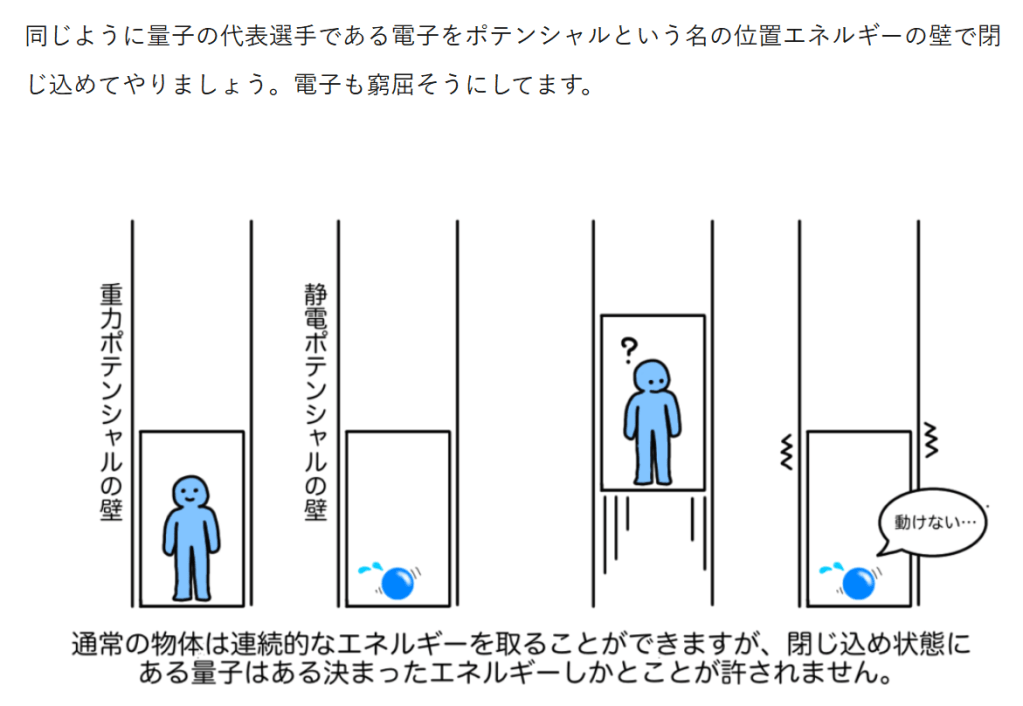
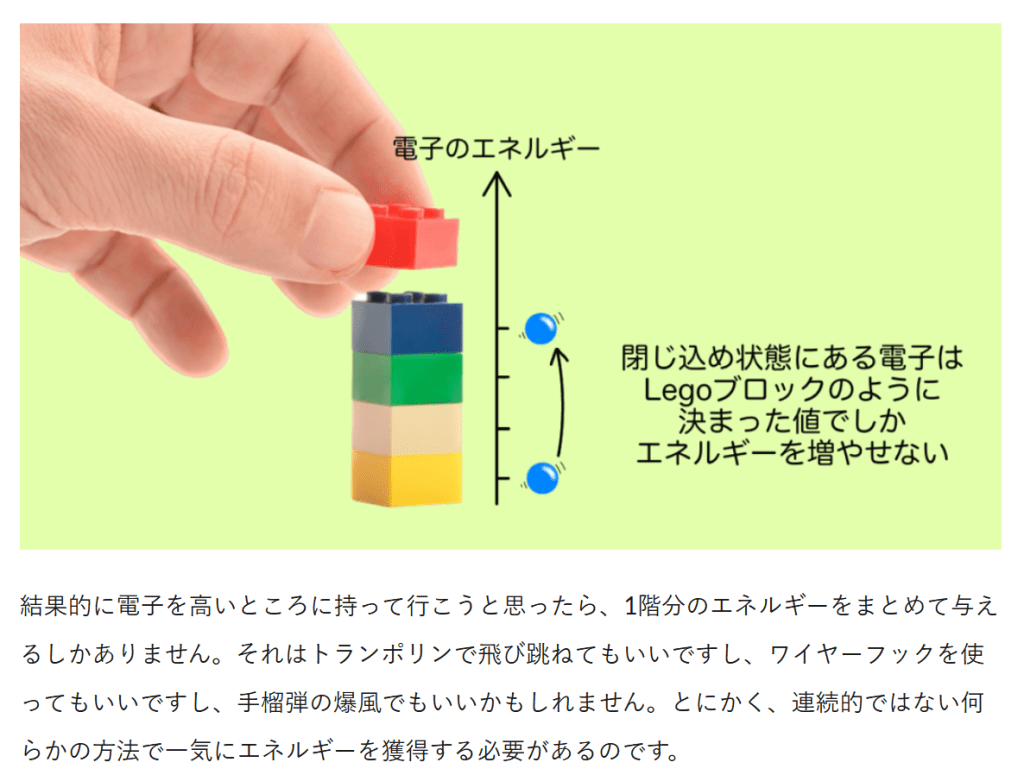
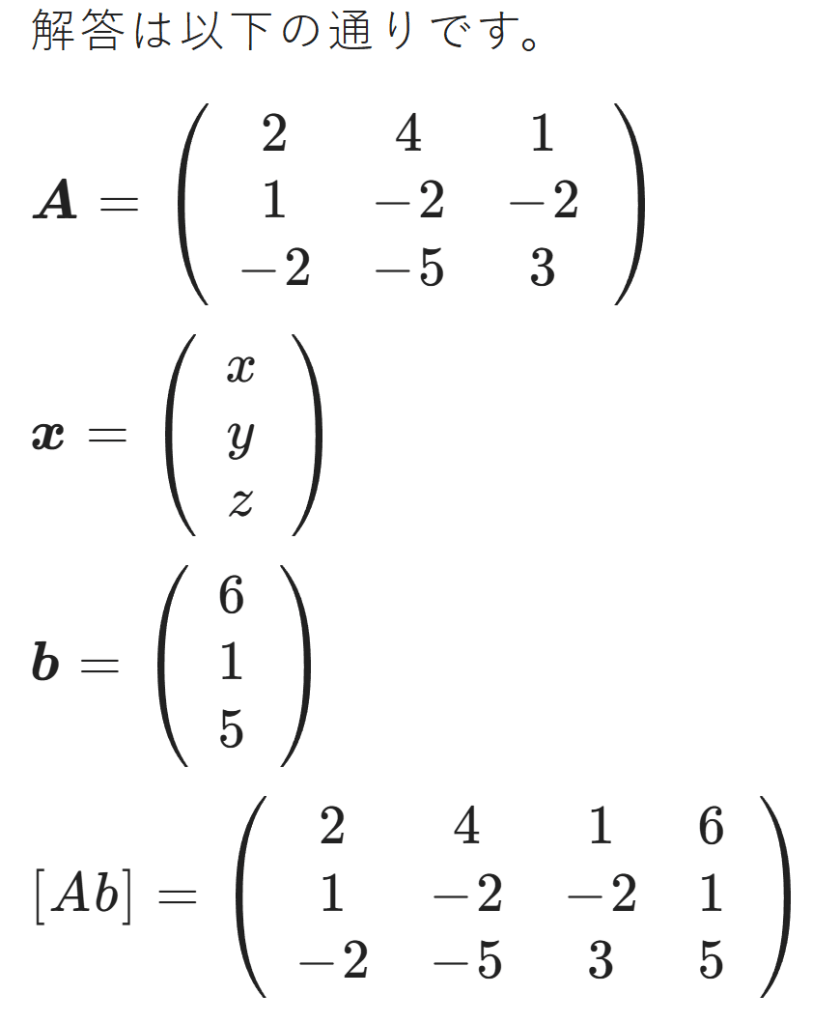月: 2025年11月
-
-
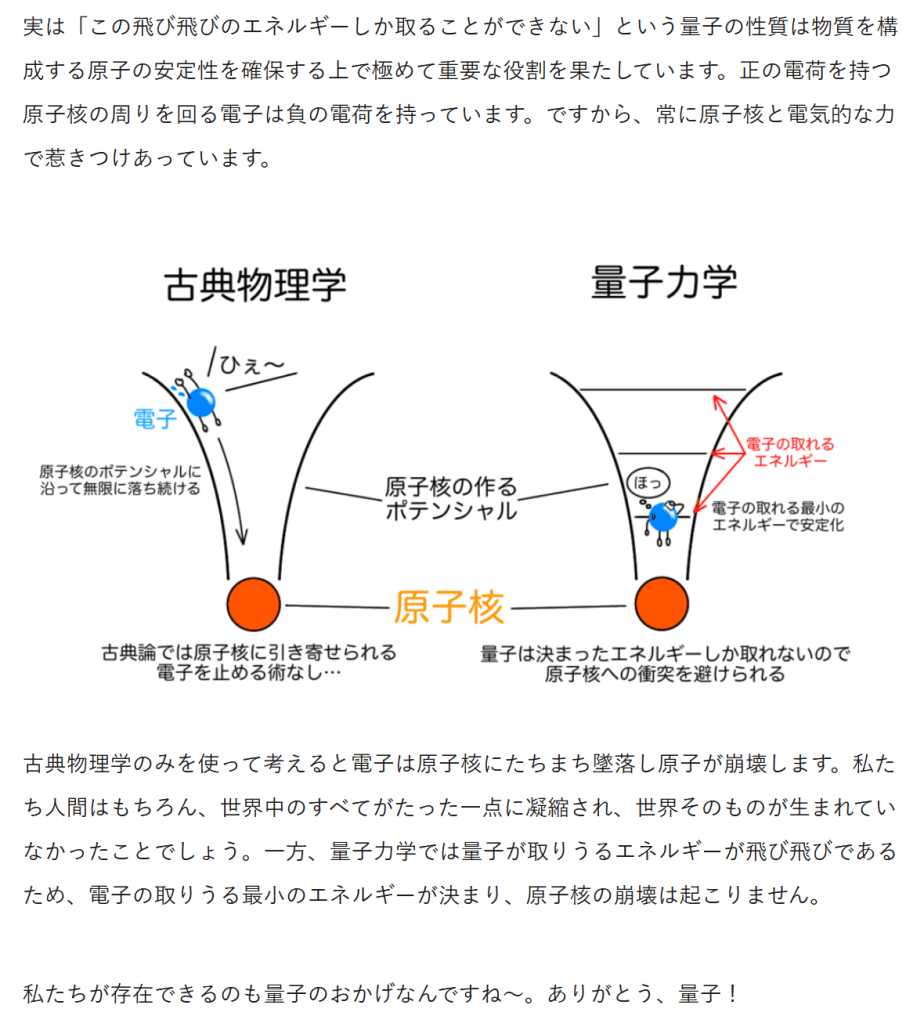
『AI による概要 量子物理学においてトポロジー的に飛び飛び(離散的)な量が出てくるのは、系の波動関数が持つ「位相」の性質が、ループや閉じた空間といった系の「トポロジー(幾何学的性質)」によって制限されるためです。
この制限は、物理量が整数値しか取れないという「量子化」を引き起こします。
量子化の理由:
境界条件と位相 量子力学では、粒子は波動関数として記述されます。
この波動関数は、物理的に意味を持つためには特定の数学的要件、特に「境界条件」を満たす必要があります。
1. 波動関数の連続性と一価性
波動関数は、空間内で滑らかに連続しており、かつ一点で一つの値しか持たない「一価関数」でなければなりません。
空間内を一周して元の場所に戻ってきたとき、波動関数の「位相」(波のどの位置にいるかを示す角度)は、元の位相と一致している必要があります。
- トポロジー的な「ねじれ」
通常の空間では、この条件は自明に満たされます。
しかし、トポロジカルな系では、電子が運動する空間や、運動量空間と呼ばれる抽象的な空間が「ループ」や「穴」を持った構造をしている場合があります。
具体例としての磁場中の電子:
外部磁場中の電子を考えた場合(量子ホール効果など)、電子の波動関数は、磁場によって通常の空間とは異なる「位相のねじれ」の影響を受けます。
このねじれの度合いがトポロジカルな量に対応します。
- 整数量子化の必然性
一価性の条件を満たすためには、この「位相のねじれ」は、(2\pi )(360度)の整数倍でなければなりません。
ちょうど、輪ゴムを指に巻き付ける回数が整数回でなければならないのと同じ論理です。
この整数の巻き数のような性質が、トポロジカル不変量(チェルン数など)と呼ばれます。
この不変量は、系の詳細な形状や不純物といった微小な変化に対して非常に頑強(ロバスト)であり、連続的に変化することはありません。
変化するためには、エネルギーギャップを閉じるような劇的な変化(相転移)が必要です。
したがって、トポロジカルな量は「整数」という飛び飛びの値しか取ることができず、これが観測される物理量(例えば、ホール伝導度など)の正確な量子化として現れるのです。
Have physicists figured out the reason that quantization is so …2023/03/19 — It’s more about functional analysis and how PDEs e…Reddit
非エルミート性に由来する新たな端状態を提案 – 工学系研究科 – 東京大学2020/11/11 — 例外点(赤色の点)の間の部分が糊付けさ れたように接着され、外乱や不純物によっては簡単には引きはがせ…東京大学大学院工学系研究科超伝導体のための新しい系統的トポロジカル不変量 – 京都大学トポロジカル不変量とは,ギャップを閉じないHkの連続変形(つまり断熱変形)で変化しな いような整数値のこと.京都大学サンプル・ 波動関数は考えている空間で「 一価連続で滑らか」でなければならない。さくらインターネットSt研 量子ホール効果とトポロジー – 名古屋大学このように,量子ホール効果はトポロジカル不変量として表現されることは,単なる式の書き換えに留まるものではなく,現象の本質…St研Have physicists figured out the reason that quantization is so …2023/03/19 — It’s more about functional analysis and how PDEs e…Reddit非エルミート性に由来する新たな端状態を提案 – 工学系研究科 – 東京大学2020/11/11 — 例外点(赤色の点)の間の部分が糊付けさ れたように接着され、外乱や不純物によっては簡単には引きはがせ…東京大学大学院工学系研究科超伝導体のための新しい系統的トポロジカル不変量 – 京都大学トポロジカル不変量とは,ギャップを閉じないHkの連続変形(つまり断熱変形)で変化しな いような整数値のこと.京都大学すべて表示
AI モードでさらに詳しくAI の回答には間違いが含まれている場合があります。 詳細高評価低評価ありがとうございましたお寄せいただいたフィードバックは、Google のサービス改善のために活用させていただきます。プライバシー ポリシーをご確認ください。
その他のフィードバックを共有問題を報告閉じるありがとうございましたお寄せいただいたフィードバックは、Google のサービス改善のために活用させていただきます。プライバシー ポリシーをご確認ください。
その他のフィードバックを共有問題を報告閉じるありがとうございましたお寄せいただいたフィードバックは、Google のサービス改善のために活用させていただきます。プライバシー ポリシーをご確認ください。
その他のフィードバックを共有問題を報告閉じるもっと見る』 -






『<紹介文>
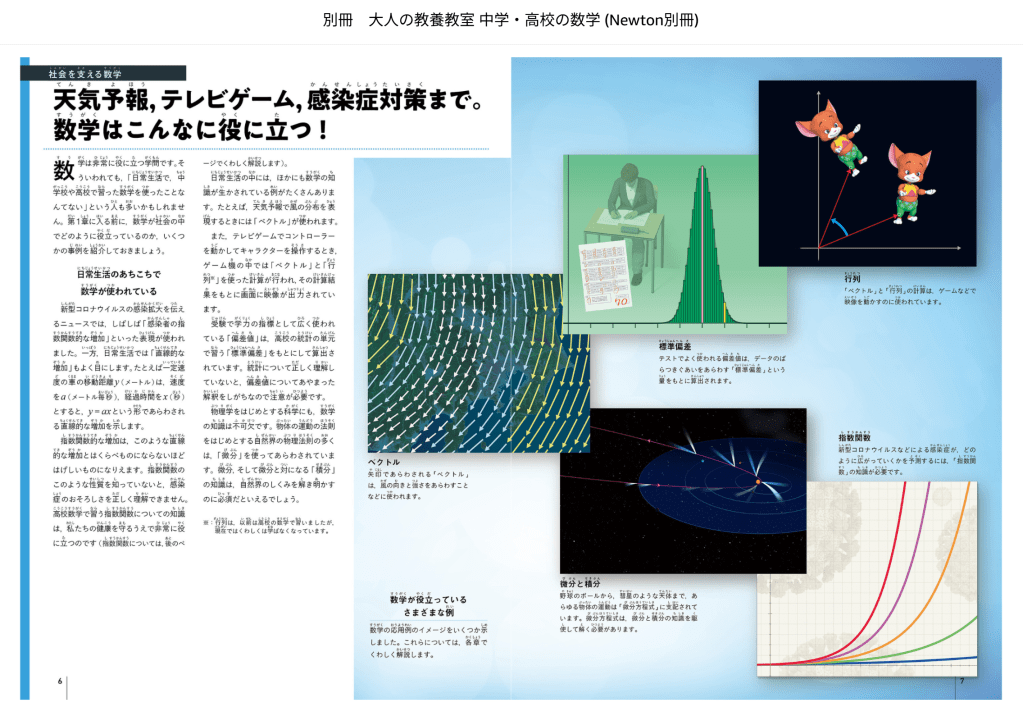
中学校や高校の授業で学ぶことは「実生活では役に立たない知識」と誤解されがちです。しかし,実際には私たちの暮らしのあちこちで役に立っています。
たとえば,「数列」の知識は最新のビデオゲームなどにも活用されていますし,「指数・対数」や「微分積分」で自然界の現象を把握することができます。
「三角関数」は土地の傾きや距離をはかることだけでなく,家電製品にも応用されているのです。
本書は,中学・高校で学ぶ数学の単元をやさしく解説するだけでなく,それらの知識からさらに一歩踏みだし,ビジネスや日常生活に数学が活用されるようすや,奥深い魅力も紹介しています。
かつて学んだ人だけでく,これから学ぶ人にも,数学を「面白い!」と感じてもらえるはずです。ぜひお楽しみください。<目次>
1 「数」と「数列」を使いこなそう
社会を支える数学
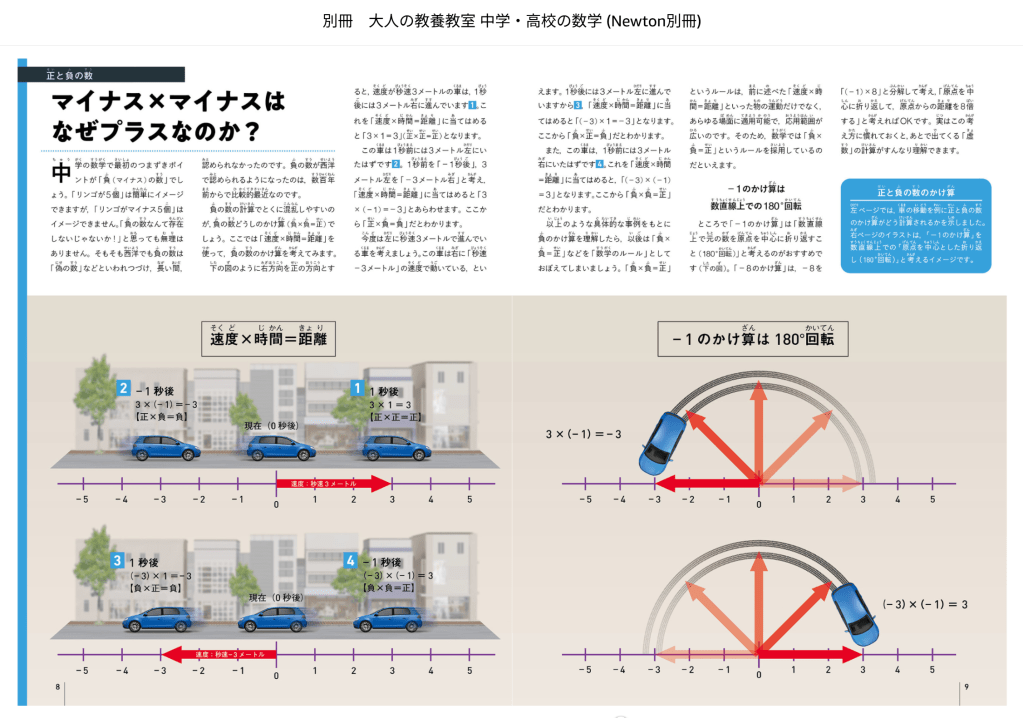
正と負の数
有理数と無理数
column 1 自然数も実数も無限個ある。では,どちらのほうが多い?
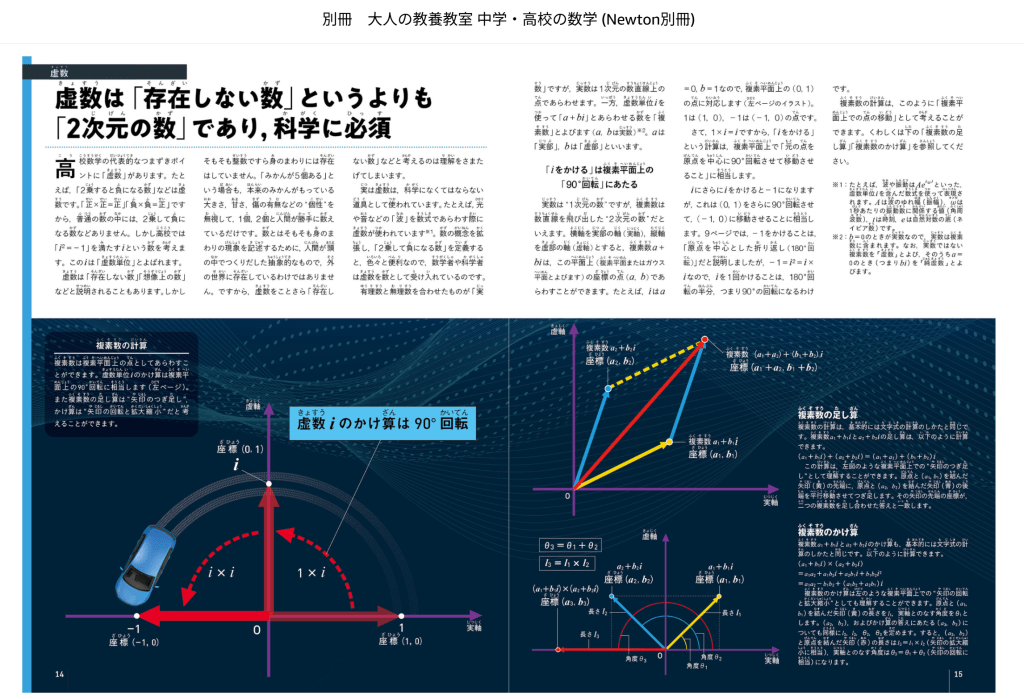
虚数
column 2 負の数の登場は数学界で驚異的な出来事だった
column 3 コピー用紙には2と3がかくれている
数列
column 4 かけ算の可視化
ベクトル
ベクトルと行列
column 5 割り算と歯車
第1章 公式集2 「図形」で空間を把握しよう
点・線・角
基本作図
三角形と四角形
column 6 円と直角三角形の不思議な関係
column 7 円の中心を探せ!
相似
column 8 「相似」で考える星の明るさ
column 9 プラトンと正多面体
第2章 公式集3 「関数」で見えないものを予測しよう
関数
指数関数
指数関数の威力
指数と対数の関係
対数関数
身近な対数
対数グラフ
三角関数 ①〜②
column 10 三角関数の起源
ソーラーパネルと三角関数
ピザを6等分にする三角比
第3章 公式集4 「微分積分」でものごとの変化を測定しよう
微分
微分の本質
積分
積分と体積
微分積分学の基本定理
微分方程式
column 11 アルキメデスの取り尽くし法
column 12 無限に小さな部分を足すという積分のアイデア
column 13 ヒーターの温度調節に微分積分を活用
第4章 公式集5 「確率と統計」でものごとの法則性をみつけよう
確率とは何か
期待値
大数の法則
ギャンブルの確率
条件付き確率
オオカミ少年
統計学とは何か
分散と標準偏差
正規分布
column 14 健康診断の基準値と正規分布
相関
相関係数
回帰分析
天気予報の確率
場合の数
コイン投げ
第5章 公式集6 社会で役立つ中高の数学
利益の比較
新製品の利益予測
利益目標から定価を設定
数に強くなる
実感できる数にする
補償額を計算する
斜めの土地をはかる
建物の傾き
column 15 最新のVRゲームが楽しめるのも三角関数のおかげ
データのグループ分け
分散投資と数学Topics 数列』
-
幾何学
https://ja.wikipedia.org/wiki/%E5%B9%BE%E4%BD%95%E5%AD%A6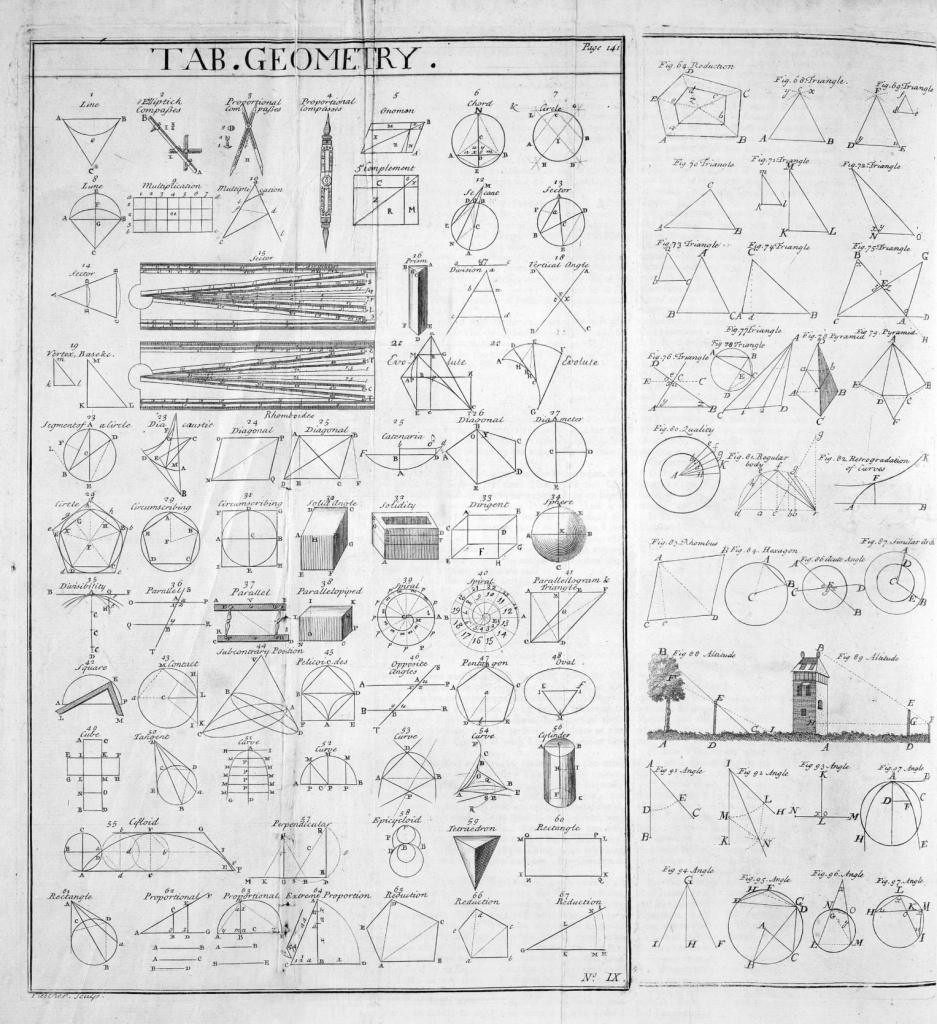
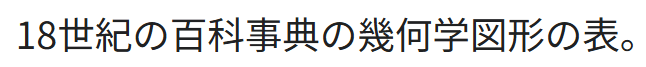













『出典: フリー百科事典『ウィキペディア(Wikipedia)』
18世紀の百科事典の幾何学図形の表。
最先端の物理学でも用いられるカラビ-ヤウ多様体の一種。現代幾何学では図も描けないような抽象的な分野も存在する。
20世紀における初等幾何学の授業風景。
幾何学(きかがく、英語: Geometry、ジオメトリー、古代ギリシア語: γεωμετρία、ゲオメトリア)は、図形や空間の性質について研究する数学の分野である[1][2]。
もともと測量の必要上からエジプトで生まれたものだが、人間に認識できる図形に関する様々な性質を研究する数学の分野としてとくに古代ギリシアにて独自に発達し[3]、これらのおもな成果は紀元前300年ごろエウクレイデスによって『ユークリッド原論』にまとめられた[2]。
その後中世以降のヨーロッパでユークリッド幾何学を発端とする様々な幾何学が登場した[3]。
単に幾何学と言うと、ユークリッド幾何学のような具体的な平面や空間の図形を扱う幾何学をさすことが多く、一般にも馴染みが深いが[3]、対象や方法、公理系などが異なる多くの種類の幾何学が存在し[1]、現代においては微分幾何学や代数幾何学、位相幾何学などの高度に抽象的な理論に発達・分化している[2][3]。
語源
クリストファー・クラヴィウスの門下生のイエズス会マテオ・リッチと中国明の徐光啓は、1607年に、クラヴィウスによる注釈付きのユークリッドの『原論』 (“Euclidis elementorum libri XV”) の前半6巻を『幾何原本』に翻訳した[4][5]。
また1680年頃にジョアシャン・ブーヴェとジャン=フランソワ・ジェルビヨンはIgnace-Gaston Pardies(英語版)の”Elements de geometrie”を同様の名前の『幾何原本』に翻訳した[6]。
一般に「幾何学」という語は、マテオ・リッチによる geometria の中国語訳であるとされるが[7]、本文中では「幾何」は「量」という意味で使われている[4][8]。
また以前は geometria の冒頭の geo- を音訳したものであるという説が広く流布していたが、近年の研究により否定されている[8]。
「幾何」という漢字表記そのものは「幾らであるか」といった程度の意味であり九章算術や孫子算経には多くこの表現が見られる。
訳語としての「幾何」は元はアリストテレス哲学にでてくる10の範疇うちの一つ「量」の訳語であり、「幾何学」についてはmathemathicaの訳語であった。
このことはジュリオ・アレーニの『西学凡』の中で明文化されて説明されている[8][9]。この語がgeometryにのみ関連付けられる習慣が定着したのは19世紀半ば以降であると思われる[8]。
歴史
以下では様々な幾何学の発展とその概要を、歴史にのっとって時系列順に述べることとする。
起源
幾何学(ジオメトリー)の語源は「土地測量」であり[注釈 1]、起源は古代エジプトにまで遡ることができる[10]。
古代ギリシャの歴史家ヘロドトスの記録[10][11]では、エジプトでは毎年春になるとナイル川が氾濫し、エジプトの砂漠に農耕を可能にする河土を運んでくるが、去年の畑の境界線はすべて流れてしまう。
そのため、印をつけた縄でまっ平らになった土地を元どおり区割りする「縄張り師」と呼ばれた測量専門家集団が現れ、土地測量術が発達した。現在、ピタゴラスの定理として知られている数学定理が、古代エジプトではすでに5000年前に経験則として知られ、縄張り師たちは3:4:5の比率で印をつけた縄を張って、畑の角の直角を取ったという[3]。
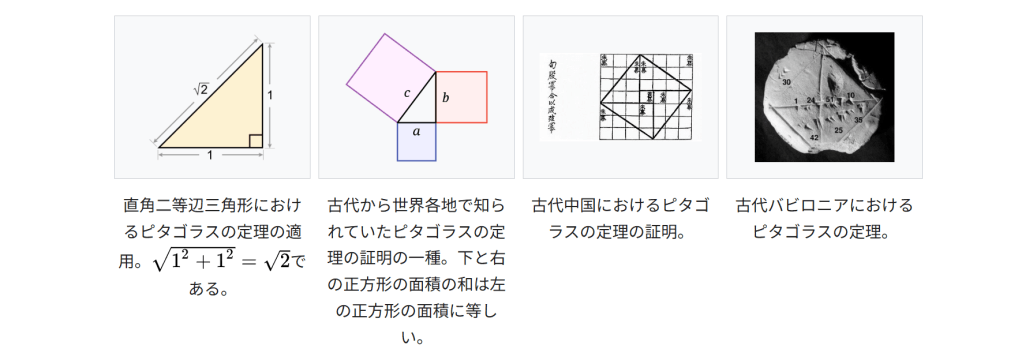
直角二等辺三角形におけるピタゴラスの定理の適用。’”
UNIQ--postMath-00000001-QINU“‘である。直角二等辺三角形におけるピタゴラスの定理の適用。
1
2
+
12
2
{\displaystyle {\sqrt {1^{2}+1^{2}}}={\sqrt {2}}}である。古代から世界各地で知られていたピタゴラスの定理の証明の一種。下と右の正方形の面積の和は左の正方形の面積に等しい。
古代から世界各地で知られていたピタゴラスの定理の証明の一種。下と右の正方形の面積の和は左の正方形の面積に等しい。古代中国におけるピタゴラスの定理の証明。
古代中国におけるピタゴラスの定理の証明。古代バビロニアにおけるピタゴラスの定理。
古代バビロニアにおけるピタゴラスの定理。古代ギリシャの幾何学
幾何学が大きな進歩を遂げた最初は、他の数学の分野と同じように古代ギリシアにおいてであった。
初期のギリシャ幾何学
人物としては、タレス、ピタゴラスなどが有名である[10]。
タレスは三角形の合同を間接測量に応用し、ピタゴラスらはこれらを証明により厳密に基礎づけた[10]。
彼らはそこで多くの定理を発見し、幅広くそして深く図形を研究したが、特に注記すべきなのは、彼らが証明という全く新しい手法を発見したことである。
数学的意味での証明の誕生と原論の成立
パピルスに記録されたユークリッド原論の断片。
パピルスに記録されたユークリッド原論の断片。原論の著者とされるユークリッド。
原論の著者とされるユークリッド。とくにピタゴラスは後のギリシャ数学者達に影響を与え、ユークリッドもその一人であった[3]。
自明な少数の原理(公理など)から厳密に演繹を積み重ねて当たり前とは思えない事柄を示していくやり方は、ユークリッドの手により『原論[12]』において完成され、後の数学の手本となった。
ユークリッドの手により証明をもとに体系化されたギリシャ数学は、曖昧さが残るエジプトやバビロニアのものより圧倒的に優位であったといえる[3]。
曖昧な経験の集積ではなく、それらを体系化された理論にまとめあげ少数の事実から全てを演繹するという手法は長らく精密科学の雛型とされ[11]、後世ではニュートンの古典力学なども同様の手法で論じられている。
このような手法は古代ギリシャにのみ誕生したが、それは何故かという問題は科学史の重大な問題である[11]。
ユークリッド原論はB.C.300年ごろに出版され、全13巻からなり、幾何学以外にも量や数論なども記述があるが、これらも幾何学的に取り扱われた[10]。
また原論は幾何学のバイブルとしてその後2000年以上にも渡って愛読され続けた[3]。
後期のギリシャ幾何学
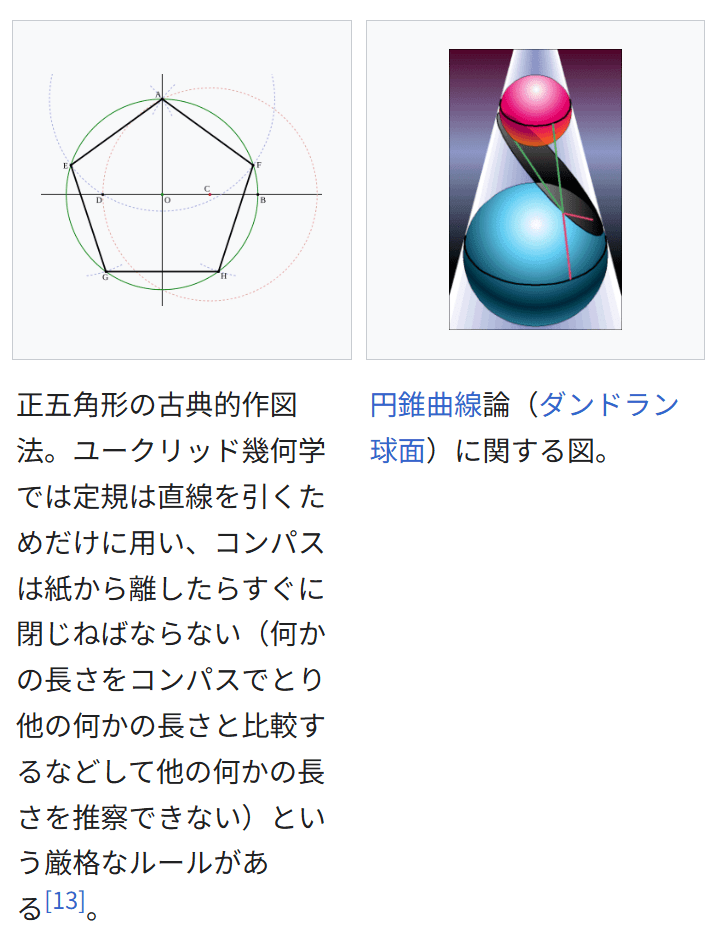
正五角形の古典的作図法。ユークリッド幾何学では定規は直線を引くためだけに用い、コンパスは紙から離したらすぐに閉じねばならない(何かの長さをコンパスでとり他の何かの長さと比較するなどして他の何かの長さを推察できない)という厳格なルールがある[13]。
正五角形の古典的作図法。ユークリッド幾何学では定規は直線を引くためだけに用い、コンパスは紙から離したらすぐに閉じねばならない(何かの長さをコンパスでとり他の何かの長さと比較するなどして他の何かの長さを推察できない)という厳格なルールがある[13]。円錐曲線論(ダンドラン球面)に関する図。
円錐曲線論(ダンドラン球面)に関する図。その後前三世紀ごろにペルガのアポロニウスによって円錐曲線論(コニカ)がまとめられ[14]、天文学の発達により前一、二世紀ごろに三角法も誕生した。
パップスは300年ごろに幾何学を中心とする古代ギリシャの数学の成果を「数学集成 (Synagoge)」にまとめあげた[10]。
とくにアポロニウスは初歩的な座標の概念をも導入し、二点からの距離の和・差・積・商が一定である曲線の集合を研究した[11]。
彼の円錐曲線の理論は、カッシーニの卵形線は17世紀に入ってから開拓されたものの他の分野のほぼ全てはアポロニウスの手によって研究された[11]。
ヨーロッパにおける幾何学
ヨーロッパでは長く、「幾何学的精神」という言葉が厳密さを重んじる数学の王道ともいうべきあり方とされた。
「幾何学的精神」という用語はパスカルによって導入された哲学用語であり、ユークリッド幾何学に見られるように、少数の公理形から全てを演繹するような合理的精神をさし、逆に全体から個々の原理を一挙に把握するという意味の「繊細の精神」の対義語として与えられた[15]。
また、エジプト王プトレマイオスが幾何学を学ぶのに簡単にすます道が無いかという問いに対しユークリッドはそんな方法はなく、「幾何学に王道無し」と言ったことからより一般に「学問に王道なし」との言葉も生まれた[16]。
ここで王道とは王のみが通れる近道の意である[16]。中世ヨーロッパのユークリッド幾何学
中世ヨーロッパでユークリッド幾何学が教えられている様子。
ヨーロッパにおいては19世紀初等までは、幾何学といえばユークリッド原論から発達した三次元以下の図形に関する数学をさしていた[10]。
ヨーロッパではルネッサンス以降はジェラルモ・カルダーノやルドヴィゴ・フェラーリに見られるように代数学が盛んであり、17世紀以降はニュートンやライプニッツらによって開かれた解析学も急激に発達したため、幾何学はこれらの分野とよく対比されることとなった[10]。
しかしルネサンス期においてはこれらに比べ幾何学の成果は乏しく[11]、当時の目立った成果を上げれば15世紀に透視図の考えを応用し射影幾何学の元となる概念が登場したり[11]、古代ギリシャでは砂に図を書いていたためか[11]運動はタブーであったが、14世紀ごろより図形を直接動かしてその変化考察するという後に解析学へと繋がる考え方も登場した[11]などが上げられる。
解析幾何学誕生
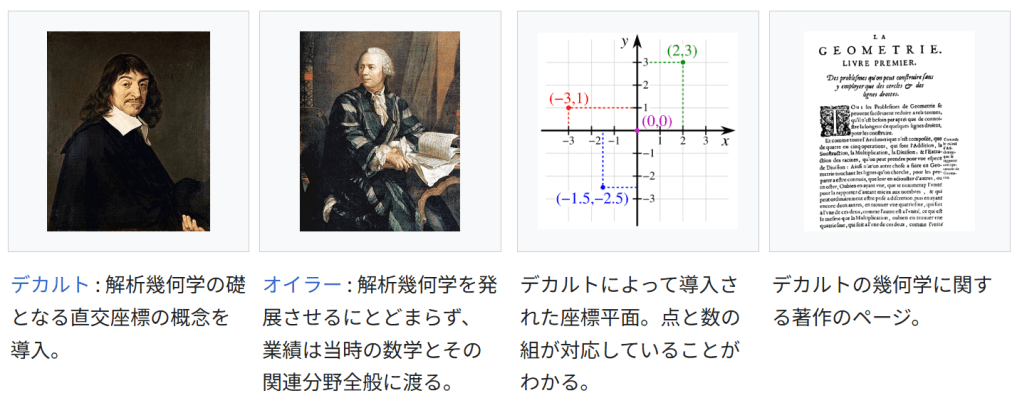
デカルトによって導入された座標平面。点と数の組が対応していることがわかる。
デカルトによって導入された座標平面。点と数の組が対応していることがわかる。デカルトの幾何学に関する著作のページ。
デカルトの幾何学に関する著作のページ。デカルト : 解析幾何学の礎となる直交座標の概念を導入。
デカルト : 解析幾何学の礎となる直交座標の概念を導入。オイラー : 解析幾何学を発展させるにとどまらず、業績は当時の数学とその関連分野全般に渡る。
オイラー : 解析幾何学を発展させるにとどまらず、業績は当時の数学とその関連分野全般に渡る。ユークリッド原論にも見られるように、数は図形として対応させて考えることもできる。
ルネ・デカルトはこの考えを拡張して直交座標系を導入し、解析幾何学を導入した[10][17]。
解析幾何学は平面や空間に座標を定めて数と図形との関係を与え、逆に数を幾何学的に扱うことをも可能とした[10]。それまでは幾何学的証明に限られた幾何学の問題を代数的に解くことも可能となったのである[10]。座標の概念はピエール・ド・フェルマーも研究していたが、欧米ではgéométrie cartésienne(デカルト幾何学、cartésienneは「デカルトの」の意)と呼ばれるようにデカルトの影響が極めて強い[11]。
例えば直交座標平面上の任意の点の原点からの距離はピタゴラスの定理によって与えられるが、これは解析幾何学においては公理である[18][19]。
解析幾何学はデカルトの哲学体系では数と図形の統一を目指したものであるが、アポロニウスの残した未解決問題、例えば三定点からの和が一定の曲線の研究なども目的とされていた[11]。
現代においてはコンピュータの画面表示などにも座標の概念が応用されている[11]。また、幾何学の問題は現代では線型代数学すら応用されて解かれることも多い[11]。
解析幾何学の方法はヨーロッパ数学において同時期に発達した代数学や解析学においても盛んに用いられ、とくに17世紀解析学の発達は解析幾何学抜きには語れないであろう[10]。
18世紀にはレオンハルト・オイラーによって解析幾何学は急激に発達させられその成果がまとめられた[20]。
オイラーの手によってアポロニウスによる古典的円錐曲線論は二次曲線や二次曲面論として解析幾何的手法を用いて代数的に書き換えられることとなった[10]。
トポロジー・グラフ理論の起源
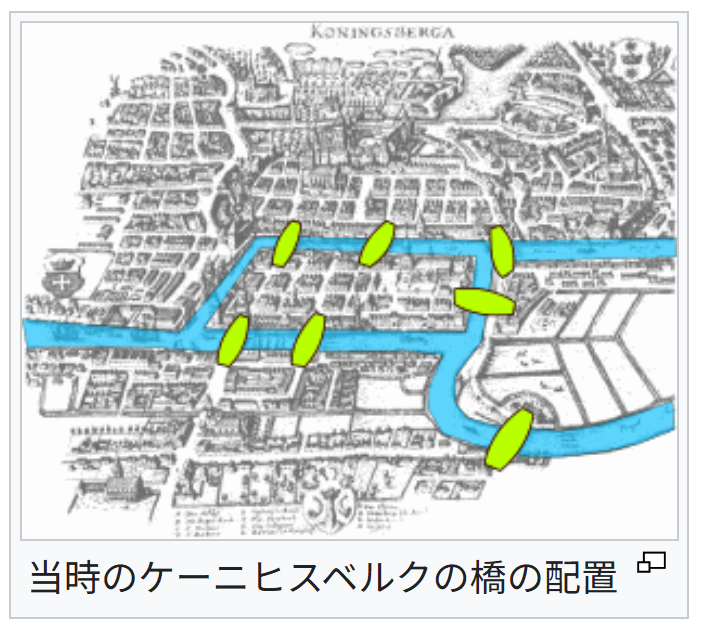
→「一筆書き」も参照当時のケーニヒスベルクの橋の配置
またオイラーは当時のケーニヒスベルクの橋を、一度渡った橋は二度と渡らないで、全ての橋を一度だけ渡ることは可能であるか?という問題より、今日の位相幾何学やグラフ理論の起源となる概念が生まれた[11]。
微分幾何学の黎明
ガウスも当時の数学関連分野全般に業績があるが、幾何学においては微分幾何学や非ユークリッド幾何学の初歩概念等に業績がある。
とはいえ非ユークリッド幾何学については論争を恐れ公表しなかった。初歩的な微分幾何学では微積分が幾何学へ応用された。
さらに18世紀末には微積分や変分学といった解析学の成果も幾何学へ応用され、ガスパール・モンジュによる曲線と曲面の微分幾何学の開拓が行われた[10]。
19世紀初頭にはガウスによって曲面の曲率などが求められ、微分幾何学が本格的に研究された[10]。
総合幾何学、射影幾何学
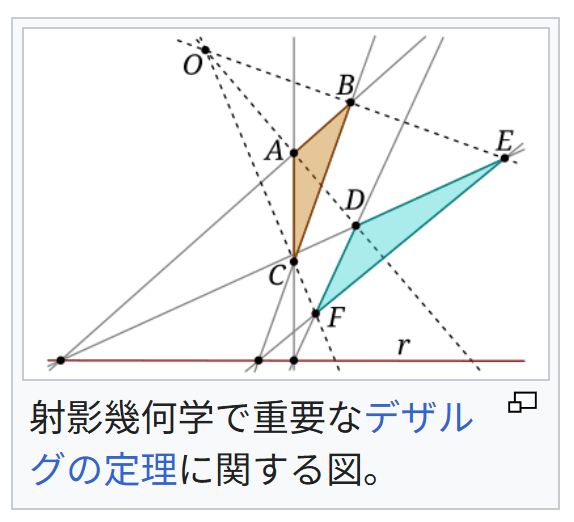
射影幾何学で重要なデザルグの定理に関する図。
このようにデカルトによってその基礎を打ち立てられ、代数的・解析的に取り扱えるという強力な手法を提供した解析幾何学であるが、解析幾何学が幾何学研究において絶対的な方法であったかといえば必ずしもそうではなかった。
解析幾何学のように座標を導入せずに、ユークリッド幾何学のように直接図形を研究する手法も解析幾何学ほどはメジャーではなかったが行われていた。
このような手法を総合幾何学(synthetic geometry) 、あるいは純粋幾何学(pure geometry)という[10]。純粋幾何学における新概念は、遠近法を発端として17世紀にジラール・デザルグとブレーズ・パスカルらによって始められた射影幾何学が挙げられる。
18世紀にはモンジュ(図法幾何学で有名である)とポンスレらにより、射影幾何学は更に研究され、19世紀に入ってもシュタイナーは総合幾何学を重視している[10]。
20世紀に入っても総合幾何学を重視した者としてコクセターが挙げられる[21][22]。ほかにも、ラングレーの問題などは20世紀に入ってから出された問題である。非ユークリッド幾何学
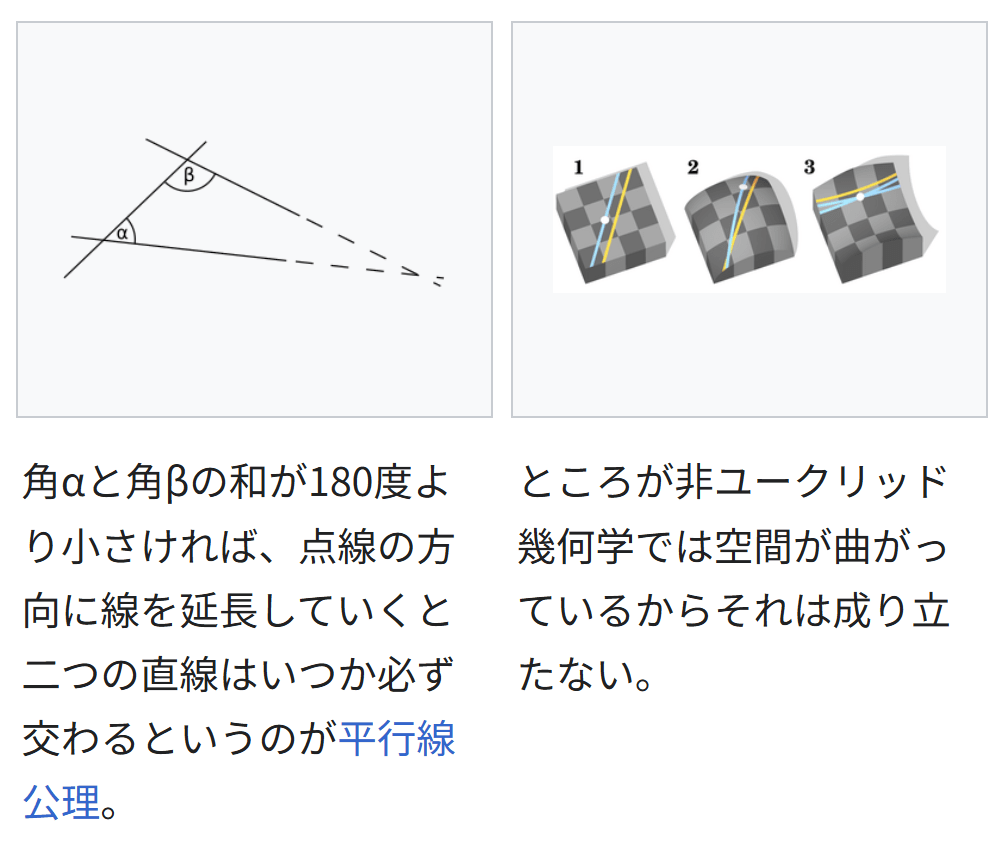
→「平行線公準」も参照角αと角βの和が180度より小さければ、点線の方向に線を延長していくと二つの直線はいつか必ず交わるというのが平行線公理。
角αと角βの和が180度より小さければ、点線の方向に線を延長していくと二つの直線はいつか必ず交わるというのが平行線公理。ところが非ユークリッド幾何学では空間が曲がっているからそれは成り立たない。
ところが非ユークリッド幾何学では空間が曲がっているからそれは成り立たない。長らく原論の平行線公準は幾何学において問題となったが、この公理を他の公理から導出しようとする試みは全て頓挫した[10]。
もし平行線公理が公理でなければ、ほかの公理系から導出できるはずだと試みられて失敗したわけである。19世紀に入ってようやく、他の公理はそのままに平行線公理のみをその否定命題に置換してもユークリッド幾何学に似た幾何学が成立することがボーヤイ・ヤーノシュ、ニコライ・ロバチェフスキーらによって示され、非ユークリッド幾何学が誕生した[10]。
非ユークリッド幾何学の無矛盾性はユークリッド幾何学の無矛盾性に依存し、後者が無矛盾であれば前者も無矛盾であるとされ、両者の差異は単なる計量テンソルの違いに過ぎないことが明らかにされた[10]。
幾何学基礎論
幾何学基礎論を研究したヒルベルト。これ以外にも広い業績がある。
幾何学は人間の図形的直感に基づいて研究されるが、直感のみに基づいて研究するわけにはいかない。
そのためあいまいな直感ではなく明確に言葉や定義によって言い表された定義や公理に基づいて幾何学を体系化する試みは既にユークリッドによってなされたのだが、現代からみればこれは不完全なものであった[23]。19世紀に入って、批判的精神や数学そのものの発達によりユークリッド幾何学の公理系が実は論理的に不完全であることが指摘された[23]。
平行線公理問題や非ユークリッド幾何学の誕生などもそのような流れの一つとしてあげられるだろう[23][24]。
数学者にとって公理系が論理的に不完全であれば、正しい方法で証明したはずの定理からも矛盾が出てしまうため、これが恐れられ一時期盛んに矛盾しない理想の公理系の探求が行われたわけである。
その探求の目的は幾何学を公理系から建設するための無矛盾な公理系の発見とその公理系によって構成される幾何学の構造、更にはそのような複数の公理系間の関係(ユークリッド幾何学と非ユークリッド幾何学との関係のような)であった[24]。
19世紀後半よりその様々な代価案が提出されてきたが[23]、最も決定的であったのが19世紀後半から20世紀初頭にはダフィット・ヒルベルトによって提唱されたものであり[23]、その成果は著書「幾何学の基礎[25][26][27]」にまとめられた[10]。
過度に抽象的な幾何学の教育への導入に抵抗し、初等幾何学の復活を唱えた[28]小平邦彦。
過度に抽象的な幾何学の教育への導入に抵抗し、初等幾何学の復活を唱えた[28]小平邦彦。ユークリッドの教育からの追放を提唱したデュドネ。
ユークリッドの教育からの追放を提唱したデュドネ。ヒルベルトは論理的整合性のために感覚から完全に分離された幾何学を唱え[3]、この本では点や線といった専門用語を机や椅子などに置換してすら成立するとまで言われたが、それにしては図が沢山あるため小平邦彦などによって批判された。
図すら一切存在しない初等幾何の基礎付けはジャン・デュドネの「線形代数と初等幾何」を待たねばならないだろう。
デュドネの本には図すら存在せず、ある意味専門用語ですら無意味であるというヒルベルトの精神を体現しているといえる。このような限界までの考察によって、公理とは「誰もが認めうる真理」ではなく、「理論を構成するための根本的要請」という考えにシフトしていった[11]。
このような極端に具体例を軽視し形式主義に走る手法は今日の公理主義的数学の先駆けと見ることができる[10]。
岡潔や小平邦彦などは極端な抽象化に警鐘を鳴らし、岡などは数学の冬の時代とまで称した。
しかし具体例や数学的直感を軽視するのが悪いことではなく、あくまで公理系の無矛盾性が大多数の数学者にとって問題であり、そのため数学の基礎や証明などの根本的部分にその批判が差し向けられたのである。
公理系が矛盾していたら正しくはじめたのにおかしな結果が出てくるかもしれないことが問題視され、この方法は幾何学基礎論から発端となったが同時期に問題となった集合論のパラドクスもあいまって[24]、幾何学にとどまらず数学基礎論としてヒルベルトらにより研究が継続されることとなる[3]。
高次元幾何学
リーマン : 複素解析の幾何学的概念(リーマン球面など)や一般相対論の元になる微分幾何学の基礎を確立。
解析幾何学では三次元ユークリッド空間の幾何学は空間幾何学 (space geometry)、または立体幾何学 (solid geometry) と呼ばれ、二次元ユークリッド空間の幾何学は平面幾何学 (plane geometry) と呼ばれる[10]。これを一般化し、n個の実数の組からn次元空間の点を定義し、それらの任意の二点間の距離空間を定めてn次元ユークリッド空間を構成することができる[10]。同様にn次元空間は非ユークリッド幾何学や射影幾何学についても定めることができる。これらのような様々な空間の研究は19世紀中頃に本格的に行われ、リーマンはn次元の曲がった空間から多様体の概念を導入し、計量として接ベクトル間の内積で曲率を定義した[10]。このような様々な幾何学はアインシュタインが一般相対性理論の研究を行った際に数学的道具を提供した[10]。より一般的には、P・フィンスラーは接ベクトルのノルムを計量とするフィンスラー空間の概念を提唱した。
現代の幾何学
幾何学と群論との関係を見いだしたクライン。
トポロジーの基礎を確立したポアンカレ。
トポロジーにおける連続的変化の一例。( https://ja.wikipedia.org/wiki/%E3%83%95%E3%82%A1%E3%82%A4%E3%83%AB:Mug_and_Torus_morph.gif )
フェリックス・クラインは幾何学に群論を応用することによって、空間Sの変換群Gによって、変換で不変量な性質を研究する幾何学を提唱した。
これをエルランゲン・プログラム[26]というが、この手法で運動群がユークリッド幾何学を定めるように、射影幾何学、アフィン幾何学、共形幾何学を統一化することができる[10]。更に19世紀末にはアンリ・ポアンカレによって、連続的な変化により不変な性質を研究する位相幾何学が開拓された[10]。
代数曲線・曲面や代数多様体が起源である代数幾何学[10]は高度に発達し、日本でもフィールズ賞受賞者も多く盛んに研究されている。
またヘルマン・ミンコフスキーによる凸体の研究は「数の幾何学」(注:数論幾何学とは異なる)の道を開いた。
20世紀前半には多様体は数学的に厳密に定式化され、ヘルマン・ワイル、エリ・カルタンらにより多様体上の幾何学や現代微分幾何学が盛んに研究された[10]。
ソフス・リーによって導入されたリー群によって、これらの様々な幾何学を不変にする変換群が与えられたが、カルタンはリー群を応用して接続の概念を導入し接続幾何学を完成させ[3]、これらの幾何学を統一化することに成功した[10]。
これはリーマンによる多様体と、クラインによる変換群の考えを統一化したとも理解できる[10]。
これは現代では素粒子物理学などの物理学の諸分野でも常識となっている。
また、代数学や解析学の発展もともなって、多様体の代数的構造と位相空間との関係を研究する大域微分幾何学、複素解析と関係する複素多様体論、古典力学の力学系と関連したシンプレクティック幾何学や接続幾何学、測度論と関連して積分幾何学や測度の幾何学的研究である幾何学的測度論の研究などもこのころにはじまった[10]。
20世紀後半になると多様体上の微分可能構造や力学系、微分作用素なども上記の幾何学とも関係しながら研究が進められた[10]。
他にも幾何構造をなすモジュライ空間や特異点を含む空間の研究、物理学と関連した研究や四色定理に見られるようにコンピューターを用いた研究も行われた[10]。
凸体の幾何学や組み合わせ幾何学の手法は現代ではオペレーションズ・リサーチなどの応用数理の分野でも用いられている[10]。
現代数学と幾何学
代数幾何学に登場する図。
現代数学では幾何学は代数学や解析学などの数学全般に広範囲に浸透しているため、これらと明確に区別して幾何学とはなにかということを論ずるのは難しいが、しかしながら図形や空間の直感的把握やそのような思考法は先端分野の研究においても重要性を失っていないといえる[10]。
下位分野
現代の幾何学の主要分野は以下は四種類である[29][30]。
位相幾何学
微分幾何学
代数幾何学
離散幾何学うち、代数幾何学は代数学の一部、離散幾何学は離散数学の一部に分類されることもある。このため、幾何学専攻・幾何学研究室を称する場合は主に位相幾何学か微分幾何学が専門であることが多い。
細かい分類は以下のようになる。
綜合幾何学
ユークリッド幾何学
初等幾何学
三角形幾何学(ドイツ語版)
幾何学基礎論
非ユークリッド幾何学
楕円幾何学
球面幾何学
双曲幾何学
非アルキメデス幾何学
射影幾何学
アフィン幾何学
解析幾何学
代数幾何学
数論幾何学
ディオファントス幾何学
微分幾何学
リーマン幾何学
シンプレクティック幾何学
複素幾何学
有限幾何学
離散幾何学
デジタル幾何学
凸幾何学
計算幾何学
フラクタル
インシデンス幾何学
非可換幾何
非可換代数幾何学脚注
[脚注の使い方]注釈
^ 術語「幾何」は古代ギリシア語: “γημετρεω” に由来し、その語義は土地測量(「古代ギリシア語: “γη”(ゲー):土地」および「”μετρεω”(メトレオ):測定」)である。この構成は 英語: “geometry” でも同じ(”geo”:土地、”metry”:測量)。
出典
^ a b 広辞苑第六版「幾何学」より
^ a b c デジタル大辞泉『幾何学』 – コトバンク
^ a b c d e f g h i j k ブリタニカ国際大百科事典2013小項目版「幾何学」より。
^ a b “幾何原本. 第1-6巻 / 利瑪竇 口訳 ; 徐光啓 筆受”. 早稲田大学図書館. 2020年12月7日閲覧。
^ 杜石然「イエズス会士と西洋数学の伝入」『中国言語文化研究』第1巻、佛教大学中国言語文化研究会、2001年7月、1-22頁、ISSN 1346-6305、CRID 1050287838661758848。
^ “The Elements of Geometry”. World Digital Library. 2020年12月7日閲覧。
^ Yibao Xu (2005). “The first Chinese translation of the last nine books of Euclid’s Elements and its source”. Historia Mathematica 32 (1): 4-32. doi:10.1016/j.hm.2003.12.002. ISSN 0315-0860.
^ a b c d 渡辺純成「満洲語資料からみた「幾何」の語源について (数学史の研究)」『数理解析研究所講究録』第1444巻、京都大学数理解析研究所、2005年7月、34-42頁、CRID 1050001201690577536、hdl:2433/47614、ISSN 1880-2818、2024年2月26日閲覧。
^ “西学凡 / 艾儒畧 答述”. 早稲田大学図書館. 2020年12月7日閲覧。
^ a b c d e f g h i j k l m n o p q r s t u v w x y z aa ab ac ad ae af ag ah ai aj ak 日本数学会編、『岩波数学辞典 第4版』、岩波書店、2007年、項目「幾何学」より。ISBN 978-4-00-080309-0 C3541
^ a b c d e f g h i j k l m n o この説は古代ギリシャ末期のプロクロスによるユークリッド原論の注釈集の冒頭にあるが、近年では批判もある。一松信、『現代に活かす初等幾何入門』、岩波書店、〈岩波講座 応用数学〉、2003年、第1章。ISBN 4-00-005454-6
^ 邦訳は「中村 幸四郎・寺阪 英孝・伊東 俊太郎・池田 美恵訳・解説、『[1]ユークリッド原論 追補版』、共立出版、2011年。ISBN 978-4-320-01965-2」など。
^ 小林昭七、『円の数学』、裳華房、1999年。ISBN 978-4-7853-1516-0
^ アポッロニオス 『円錐曲線論』 ポール・ヴェル・エック仏訳、竹下貞雄和訳、大学教育出版、2009年1月。ISBN 978-4-88730-880-0。
^ 大辞林「幾何学的精神」より
^ a b 大辞林「学問に王道なし」より
^ R. Descartes, Géométrie, Paris, 1637 (Œuvres, IV, 1901)
^ 遠山啓、『関数を考える』、岩波書店、〈岩波現代文庫〉、2011年、149頁。ISBN 978-4-00-603215-9
^ 朝永振一郎著、江沢洋編、『物理学への道程』、みすず書房、〈始まりの本〉、2012年、349頁。ISBN 978-4-622-08365-8 C1342
^ レオンハルト・オイラー著、高瀬正仁訳『オイラーの解析幾何』、海鳴社、2005年。ISBN 4-87525-227-7
^ シュボーン・ロバーツ著、糸川洋訳、『多面体と宇宙の謎に迫った幾何学者』、日経BP社、2009年。ISBN 978-4-8222-8382-7
^ コクセター著、銀林浩訳、『幾何学入門上・下』、筑摩書房、〈ちくま学芸文庫Math&Science〉、2009年。上巻ISBN 978-4-480-09241-0、下巻ISBN 978-4-480-09242-7
^ a b c d e 日本数学会編、『岩波数学辞典 第4版』、岩波書店、2007年、項目「幾何学基礎論」より。ISBN 978-4-00-080309-0 C3541
^ a b c ブリタニカ国際大百科事典2013小項目版「幾何学基礎論」より。
^ D. Hilbert, Grundlagen der Geometrie, Teubner, 1899, 第 13 版 1987
^ a b D・ヒルベルト、F・クライン著、寺阪英孝・大西正男訳、解説・正田建次郎、吉田 洋一監修、『ヒルベルト幾何学の基礎、クライン・エルランゲン・プログラム』、共立出版、〈現代数学の系譜 7巻〉、1970年。ISBN 978-4-320-01160-1
^ D・ヒルベルト著、中村幸四郎訳、『幾何学基礎論』、筑摩書房、〈ちくま学芸文庫 Math&Science 〉、2005年。ISBN 978-4-480-08953-3
^ 小平邦彦著、上野健爾解説、『幾何への誘い』、岩波書店、〈岩波現代文庫〉、2000年。ISBN 4-00-600007-3 C0141
^ 砂田利一『現代幾何学の流れ』2007年。
^ TANAAKK. “幾何学の分類 – TANAAKK”. 2025年10月18日閲覧。
関連項目
哲学
ギリシア哲学
古代エジプト哲学
古代ギリシア
古代エジプト
数学
測量
幾何学構成的絵画
幾何学模様
人工知能[1]
外部リンク
ウィキペディアの姉妹プロジェクトで
「幾何学」に関する情報が検索できます。
ウィクショナリーの辞書項目
コモンズのメディア
ウィキニュースのニュース
ウィキクォートの引用句集
ウィキソースの原文
ウィキブックスの教科書や解説書
ウィキバーシティの学習支援
Portal:数学
ポータル 数学
Geometric ArtsAesthetic Geometry Site
Weisstein, Eric W. “Geometry”. mathworld.wolfram.com (英語).
Geometry – PlanetMath.(英語)
“Geometry”, Encyclopedia of Mathematics, EMS Press, 2001 [1994]
『幾何学』 – コトバンク
表話編歴
数学
表話編歴
幾何学の主要なトピックス
典拠管理データベース ウィキデータを編集
^ “AlphaGeometry, a System That Nears Expert Proficiency in Proving Complex Geometry Theorems” (英語). AlphaGeometry, a System That Nears Expert Proficiency in Proving Complex Geometry Theorems (2024年1月24日). 2024年1月26日閲覧。
カテゴリ: 幾何学数学に関する記事最終更新 2025年10月18日 (土) 07:45 (日時は個人設定で未設定ならばUTC)。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。』 -
『AI による概要
射影という考え方は、幾何学の統一的な理解を可能にし、新しい数学分野の創設につながったという歴史的に重要な役割を果たしました。
特に、消失点という「無限遠点」の概念を導入したことで、ユークリッド幾何学とは異なる視点を提供しました。
主な役割は以下の通りです。
透視図法から射影幾何学へ:
ルネサンス期の芸術家や建築家による遠近法(透視図法)の研究が、射影の数学的な探求の出発点となりました。
画家たちは、奥行きのある現実的な絵画を描くために、空間内の物体が平面のキャンバスにどのように映るかを経験的に研究し、消失点の概念を発見しました。
17世紀にジェラール・デザルグらがこの芸術的な技法を理論的な幾何学へと発展させ、射影幾何学が誕生しました。
この幾何学では、長さや角度ではなく、図形の接続関係(例えば、直線上の点の位置関係や交わり)に焦点が当てられました。「無限遠」の数学的導入:
平行な線路が遠くで一点(消失点)に集まって見える現象を数学的に説明するため、「無限遠点」や「無限遠直線」という概念が導入されました。
これにより、通常のユークリッド平面を拡張した「射影平面」という新しい空間が定義され、平行線も無限遠点で交わるとして扱えるようになり、幾何学の記述がより統一的かつ簡潔になりました。
幾何学の一般化と統一:
射影幾何学は、従来のユークリッド幾何学をより広い視点から捉え直すことを可能にしました。
アイザック・ニュートンは、射影の考え方を用いて様々な3次曲線を統一的に分類しました。
解析幾何学(座標幾何学)の手法も取り入れられることで、双対性といった強力な概念が生まれ、数学全体の発展に大きく寄与しました。
このように、射影という考え方は、視覚芸術の実践的な探求から始まり、ユークリッド幾何学の枠を超えた新しい幾何学の体系を築き、現代数学においても重要な役割を果たす基礎概念となりました。
Geometry: A History From Practice to Abstraction | NRICH
2011/01/31 — In 1639, Girard Desargues (1591-1661) wrote his gr…NRICH
射影幾何の考えかた – 東京大学
2023/10/08 — * 午後の講演では射影幾何と呼ばれる、これまでに習った平面幾何(ユークリッド幾何) とは性質の異なる…Graduate School of Mathematical Sciences
Projection (mathematics) – Wikipedia
The concept of projection in mathematics is a very old one, …Wikipedia
すべて表示
AI モードでさらに詳しく』 -
-
『AI による概要
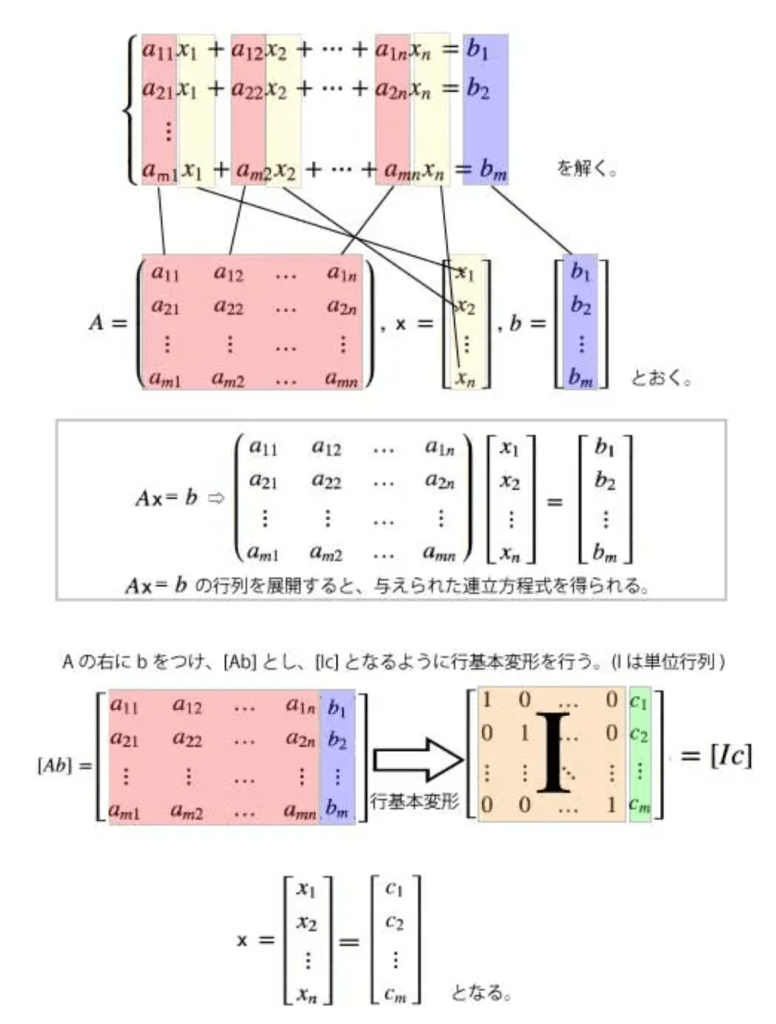
掃き出し法とは、連立一次方程式を解くための系統的な方法で、拡大係数行列(連立方程式をまとめて1つの行列にしたもの)に行基本変形を繰り返し適用して解を求める手法です。
この方法により、変数の数が増えても効率的に解を求めることができ、さらに逆行列を求めたりすることも可能です。
特徴
拡大係数行列を使用する: 連立方程式を拡大係数行列という形にまとめます。
行基本変形を適用する: 以下の3つの操作を繰り返し行い、行列を簡約化していきます。
ある行に、他の行の何倍かを加える(引く)。
ある行に0でない数をかける(割る)。
解を求める: 最終的に行列を「行標準形」と呼ばれる形に変形することで、連立方程式の解を読み取ります。手順が定まっている: 従来のような式を変形する感覚的な判断ではなく、決まった手順で計算できるため、複雑な方程式でも効率的に解くことができます。
利点
変数の数が増えても計算を系統的に行えるため、効率的に解を求めることができます。
連立方程式の解を求めるだけでなく、行列の逆行列を求めることにも応用できます。
計算手順が明確なため、誰が計算しても同じ結果が得られます。
21:46
線形代数②(掃き出し法)連立方程式は考えて解くな!【大学 …YouTube·10分で単位が取れる、理系科目のサクっと講義
掃き出し法 – Kanazawa Institute of Technology
2022/06/23 — 連立1次方程式の解の求め方に消去法がある. この消去法を拡大係数行列を用いて計算する方法を掃き出し法…KIT 金沢工業大学
掃き出し法を用いた逆行列の求め方を例題で解説 – AVILEN
2024/04/29 — 掃き出し法とは 掃き出し法とは、以下のように説明できます。 … 行列Aの右隣に単位行列Iをつけ、…AVILEN
掃き出し法による連立一次方程式の解き方 | 問題と解説
掃き出し法 とは 拡大係数行列 を利用して連立一次方程式を解く手法です。光学技術の基礎用語
掃き出し法 – Kanazawa Institute of Technology
2022/06/23 — 連立1次方程式の解の求め方に消去法がある. この消去法を拡大係数行列を用いて計算する方法を掃き出し法…KIT 金沢工業大学
掃き出し法・ガウスの消去法(連立1次方程式の解法) – ワイズ
2023/04/10 — ゆえに と の解集合もまた一致するため、 を解く代わりに を解くことができます。 は行標準形であるた…wiis.info
AI モードでさらに詳しく 』
-
不動産業界の3大タブー行為、違反行為
https://retech-network.com/posts/detail/840『2022-02-28 10:14
不動産業界の3大タブー行為、違反行為
不動産業界にもタブー行為や禁止行為は存在します。
また、不動産業界は関係する法律も多いだけに、知らないと法律に触れてしまう場合があります。
今回は、今すぐ知っておくべき!不動産業界のタブー行為、違反行為をご紹介します。
〈目次〉
不動産業界の3大タブー行為
抜き
飛ばし
囲い込み不動産業界で起こりやすい違反行為
顧客情報の漏えい
重要事項の説明不足
宅建士以外の重要事項説明
おとり広告
捨て看板・電ビラ不動産業界で禁止行為を犯すと…
不動産業界の3大タブー行為
不動産業界には3大タブー行為と呼ばれている・抜き
・飛ばし
・囲い込み
という行為があります。
これら3つを詳しく解説します。
抜き
不動産業界における抜き行為とは依頼者である売主・買主・貸主・借主と不動産業者との間に媒介契約が結ばれているにも関わらず、別の不動産業者が「手数料を安くする」「購入者を紹介する」などと誘い依頼者と新たに契約を結ぶ行為です。
要するに契約が決まった他社のお客様にアプローチをかけることを言います。
契約者からすれば二重契約となる場合や、先に依頼した不動産業者との契約を破棄し後から来た不動産業者との契約を進めることとなります。
これはお客様を「引き抜く」行為となり業界ではタブーとされています。
この抜き行為は、法律上の違反とはなりませんが、してもいいという法律もありません。
法律に触れなくても、民事として損害賠償請求や名誉毀損などの対象となる可能性はあります。
不動産業者同士のマナーとして抜き行為はやめましょう。
飛ばし
飛ばしとは不動産業界で複数の意味で使われます。
一つ目は「お客様だけで物件に行かせること」
不動産業者の同伴なしにお客様を物件へ飛ばすことから「飛ばし」と言われます。
勝手に物件を見て、勝手に決めてもらって、手数料はきっちり頂く。
この飛ばし行為はトラブルに発展しやすく、良い行為とはされません。
もう一つは「不動産仲介業者を飛ばす」意味として使用されます。
【飛ばし行為の例】
①A社へ行き物件を紹介してもらい、その後B社へ行き同様の物件を契約する
②A社へ行き物件の内見をし、その後B社へ行き同様の物件を契約
など、初めに物件を紹介してもらった仲介業者から情報を得て、他の不動産業者へ依頼したり直接売主に交渉しにいくこと「飛ばし」行為と言います。
直接、売主に契約をして仲介手数料の支払いを免れようとする事を「飛ばし」や「仲介業者飛ばし」などと言われています。
囲い込み
お客様から不動産売却の依頼をうけた不動産会社は、その物件を自社だけで販売せず、不動産業界全体で情報を共有し、多くの会社で販売できるようにしなくてはなりません。
売却の委任契約を受けた不動産会社が、故意に情報を隠したり独占することは法律で禁じられています。
媒介契約を受けた場合、決められた期間内に「物件情報を指定流通機構(レインズ)へ登録する事」が義務付けられています。
しかし、売主から売却依頼を受けた不動産屋さんが、自分で買主を見つけたいがために、他社の不動産屋に物件を紹介しない「物件の囲い込み」が行われていることも事実です。
この囲い込みはレインズへ登録はするが、他社へは紹介しないことを指します。
つまり、別エリアの他社の不動産会社から「〇〇物件を案内させて欲しい」という依頼があっても、「申し込みが入った」と嘘をつき他社への紹介を断るのです。
売却物件の仲介を依頼された不動産会社は仲介手数料が収入源です。
その手数料を売主と買主の双方からもらうために不動産会社が売却物件を自社で抱え込み、他社には紹介しないという「囲い込み」は売主に対する裏切りの行為となります。
不動産業界で起こりやすい違反行為
不動産業界で起こりやすい違反行為にはどのようなものがあるのでしょうか。
もしかすると、意図していないのにも関わらず違反行為となっている場合もありますので、注意が必要です。
顧客情報の漏えい
不動産業者には守秘義務があります。
不動産業者が扱っている個人情報は、住所や電話番号など個人の生活実態や住居を特定できるものです。
顧客の住所や電話番号が外部に流出することで、ストーカーなどの深刻な被害に繋がる可能性があるため、個人情報の取り扱いには慎重を期す必要があります。
例え知り合いであっても絶対に顧客の情報を漏らしてはいけません。
SNSで呟く行為も禁止されています。
重要事項の説明不足
不動産業者が顧客と契約を結ぶ際は、締結前に「重要事項の説明」が義務付けられています。
「重要事項の説明」は、たとえ顧客が望まなくても説明を省いてはならないのです。
不動産の取引には、大きな金額が動き、複雑な法律上の手続きも伴います。
重要事項説明は、買主・借主が購入や賃借の前に宅地建物とその取引条件に関する重要事項を理解し、十分な情報を得た上で購入や賃借をするかどうかを判断できるようにするための説明です。
2017年10月1日より、賃貸借契約に関する取引に限定してIT重説が可能となりました。
IT重説とは、テレビ会議などのITを活用して行う、賃貸借契約における重要事項説明を指します。
従来は宅地建物取引士自らが対面で説明を行わなければいけませんでしたが、対面と同様に説明や質疑応答が行える双方向性のある環境であれば、自宅などにいながらパソコンなどで重要事項説明を受けられるようになりました。
重要事項説明では、説明すべき事項は複雑多岐にわたり、口頭で理解してもらえる内容ではありません。
そこで、いかなる重要事項説明においても、書面を交付して説明することが法律上の義務とされています。
宅建士以外の重要事項説明
不動産取引で重要な書類である重要事項説明書の作成は宅建士以外でも行えます。
しかし、実際に重要事項説明を行う行為は宅地建物取引士(宅建士)である必要があります。
これを破ると、宅建業法違反となり個人でなく、会社全体の違反行為となります。
不動産会社で働く社員の必須資格である宅建士。
不動産事務所では「業務に従事する者」5人につき1人以上の割合で、専任の宅地建物取引士を設置することが義務付けられています。
忙しい日々に追われながら宅建士合格を目指して勉強している方も多いのではないでしょうか。
コロナ禍ということもあり宅建講座に通うことすら難しいですね。
今、需要が伸びているのが「宅建士」の通信講座をスマホで受講できる不動産テック「受かっちゃえ宅建」です。
宅建士の試験合格率は15%前後と決して簡単ではありませんが、今後需要の増す資格の一つですので挑戦してはいかがでしょうか。
関連記事:【宅建試験直前】見直すべきポイント!
関連記事:宅建の5点免除とは?5点免除を受けるための方法・メリット・デメリットとは
おとり広告
おとり広告とは、顧客を集めたり、手持ち物件を売るために、売る意思のない条件のよい客寄せ用の物件等の広告を指します。
要するに、既に募集が終了している物件や架空の物件をインターネット上に出して客を引く悪徳不動産屋の広告です。
この行為は、宅地建物取引業法32条に違反し、不動産の表示に関する公正競争規約21条で禁止されています。
【おとり広告の例】
・実在しない架空物件
・実在はするが売却済みの物件
・オーナーから売却依頼のない物件の広告
これら、おとり広告は主に集客に使われ、接客時に他で成約してしまった等を理由に他の物件に誘導するなどの例が多く挙げられています。
また、インターネット広告において、成約済み物件を広告の更新予定日を過ぎても削除せず、サイト上に掲載し続けることもおとり広告としてみなされることになります。
捨て看板・電ビラ
電柱にくくり付けられた捨て看板や、同じく電柱に貼られたチラシ(電ビラ)などによる不動産広告は相変わらず多く、よく目にすることもあるでしょう。
このような「許可なく貼られたチラシ広告」を捨て看板・電ビラと言います。
捨て看板・電ビラは、軽犯罪法、道路交通法、それぞれの自治体が定める屋外広告物条例などに違反するほか、自治体によっては景観条例、迷惑防止条例などにも抵触する場合があります。
捨て看板・電ビラを取り付けるところを警察官に目撃されれば現行犯として捕まることになるため、チラシ自体に会社名は表示せず、携帯電話番号のみを記載するケースが多いのです。
東京都が毎年秋に実施している「捨て看板等の共同除却キャンペーン」では、除却された違反広告物の大半を不動産業が占めています。
いかに、捨て看板・電ビラの違反行為が多いか一目瞭然ですね。
不動産業界で禁止行為を犯すと…
不動産業界は決まり事や法律が多く存在します。
特に、重要事項説明には明確なルール・義務が存在し、かつ説明必須の内容も多いので意図せず違反してしまう人がいます。
故意であってもなくても違反は違反なので、会社が指導や罰則を受ける場合があります。
こうした違反行為・禁止行為を繰り返すことでトラブルの元となりお客様の信用だけでなく、他社からの信頼もなくなりますので絶対に止めましょう。
〈参考〉
TATSUJIN JOURNAL:事故物件の告知に判断基準|人の死の告知に関するガイドライン
TATSUJIN JOURNAL:してはいけない!不動産業界のタブーや違反行為
イエフリコラム:不動産業界のタブーである「囲い込み」「売り止め」とレインズ(物件データベース)について
コンシスト:不動産業のコンプライアンスとは?具体的な違反内容を徹底解説! 』
-
『AI による概要
ニューヨークの不動産ビジネスで成功するには、現地の市場動向を読む力、専門知識、高いコミュニケーション能力と行動力が不可欠です。
特に、世界中から投資が集まる競争の激しい市場であるため、一般的な不動産スキルに加えて、ニューヨーク特有の事情に精通している必要があります。
以下に、必要な資質をまとめます。
- ニューヨーク市場に特化した専門知識
現地の市場動向を読む力:
ニューヨークは多様な文化が混在し、街の流れが速く変化します。
ミッドタウンのような特定のエリアの不動産価格が非常に高いなど、地域ごとの特性や最新の市場トレンドを正確に把握する能力が重要です。
法規制と契約実務の知識:
不動産取引には、現地の法律(宅建業法、民法など)に関する深い知識が不可欠です。
特に商業不動産のリース契約では、貸主側の審査条件や解約時の違約金など、日本とは異なる複雑な条件が存在するため、契約交渉に精通している必要があります。
関連資格の取得:
業務を行うには、ニューヨーク州の不動産免許(エージェントまたはブローカー)が必要です。
また、米国不動産鑑定士(MAI)やCPM(不動産管理の専門家)などの専門資格は、顧客からの信頼獲得や国際的なビジネス展開に役立ちます。
- 高度なビジネススキルと対人能力
顧客目線でのコミュニケーション能力:
多様なバックグラウンドを持つ顧客(投資家、テナントなど)のニーズを正確に理解し、明確で分かりやすい提案を行う能力が求められます。
交渉力とプレゼンテーション能力:
複雑な取引や厳しい条件交渉を円滑に進めるための高い交渉スキルが必要です。
物件提案を成功させるには、優れたプレゼンテーション能力も重要になります。
迅速な行動力と忍耐力:
競争が激しく動きの速い市場では、機会を逃さずに迅速に対応する行動力が成功の鍵となります。
また、取引が長期化したり難航したりすることもあるため、忍耐強くやり遂げる力も重要です。
情報収集能力:
不動産市場のトレンド、新しい規制、競合物件の情報などを常にアップデートするための高い情報収集能力が求められます。
- マインドセット
プレッシャーへの耐性:
高額な取引が多く、市場変動も大きいため、プレッシャーの中でも冷静に判断し、目標達成に向けて努力できる精神的な強さが必要です。
向上心:
不動産ビジネスは常に変化しているため、新しい知識やスキルを継続的に学び、自己成長を目指す意欲が重要です。
米国不動産鑑定士になるには|大学・専門学校のマイナビ進学
米国不動産鑑定士(MAI)とは、アメリカが認定する資格名称。 米国内の不動産を鑑定することができるが、世界的にも認知され…マイナビ進学
米国における事業進出マニュアル - 商業不動産賃貸 -
また、新しいテナントの財務状況や 事業規模、実績などに対する貸主側の審査が条件とされることもあります。 そのような条件が…ジェトロ(日本貿易振興機構)
不動産営業職で最初に覚える基礎知識、押さえておきたい営業スキル …
2025/06/23 — 不動産営業の仕事には、法律の知識が欠かせません。 営業活動を行うときは宅建業法が絡みますし、契約のと…recruit.openhouse-group.com
すべて表示
AI モードでさらに詳しく
AI の回答には間違いが含まれている場合があります。 詳細 』 -
『AI による概要
ニューヨークの不動産ビジネスは、世界的な金融センターとしての高い需要と、それに伴う巨大な投資規模、複雑な取引構造が主な特徴です。
主な特徴は以下の通りです。
世界有数の投資市場: ニューヨーク、特にマンハッタンは世界の主要都市の中でも特に不動産価値が高く、世界中から富裕層や機関投資家が集まる投資対象となっています。そのため、取引される金額は非常に大規模です。
安定した賃貸需要と低い空室リスク: 人口密度が高く、ビジネスや観光での短期・長期滞在者が多いため、住宅・商業用ともに賃貸需要が非常に安定しており、空室率が低い傾向にあります。
複雑な規制と独特な慣行: アメリカの他の都市と比較して、賃貸規制(レント・コントロールなど)やゾーニング規制などが複雑で、独自の商慣行も存在します。また、物件の種類(コンドミニアム、コーポラティブなど)によって所有形態や取引ルールが大きく異なる点も特徴です。
開発プロジェクトの規模と影響力: 大規模な再開発プロジェクトが多く、これらのプロジェクトは都市の景観や経済に大きな影響を与えます。政治的な繋がりやロビー活動がビジネスに直結することもしばしばあります。
スピード感と競争の激しさ: 市場の動きが非常に速く、情報戦の側面も強いです。迅速な意思決定と実行力が求められます。
トランプ前大統領やジャレッド・クシュナー氏のような不動産ビジネス出身者は、こうした非常に競争的で大規模なビジネス環境の中で、交渉力や資金調達能力、政治的コネクションを駆使して成長してきました。
彼らの中東政策やロシア政策への関与の背景には、こうしたビジネスを通じて培われた、通常の外交ルートとは異なる独自のネットワークや交渉スタイル、ビジネスライクな視点があるとされています。
ニューヨーク不動産投資完全ガイド:魅力、リスク、成功の秘訣
2025/02/27 — 安定したインカムゲイン ニューヨークは高い賃貸需要を持つ都市で、安定した賃貸収入(インカムゲイン)が…asset-ocean.com
ニューヨーク不動産投資の特徴とは?メリットや不動産事情
2019/04/14 — 世界の都市ランキングで常に上位にあるニューヨークは世界の金融センターであり、政治・経済、ビジネス、フ…米国投資協会
世界の不動産情報 ~ニューヨークのオフィス賃貸借慣行
2016/06/27 — 賃貸面積が増える? 賃料はずっと上がり続ける?OwnersBook
すべて表示
AI モードでさらに詳しく
AI の回答には間違いが含まれている場合があります。 詳細 』