群 (数学)
https://ja.wikipedia.org/wiki/%E7%BE%A4_(%E6%95%B0%E5%AD%A6)

『出典: フリー百科事典『ウィキペディア（Wikipedia）』

この記事は検証可能な参考文献や出典が全く示されていないか、不十分です。出典を追加して記事の信頼性向上にご協力ください。（このテンプレートの使い方）
出典検索?: “群” 数学 – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2015年9月)
代数的構造 → 群論

群論

基本概念
有限群
離散群格子
位相 / リー群
代数群
代数的構造
群に似た構造
群
半群 / モノイド
圭
準群とループ
アーベル群マグマリー群
群論
環に似た構造
束に似た構造
加群に似た構造
代数に似た構造
表話編歴

数学、特に抽象代数学における群（ぐん、英: group）とは、一つの集合と、その集合上に閉じて定義された一つの二項演算で構成される組（代数的構造）であり、ただしその二項演算は結合法則、単位元、逆元を全て有する。

マグマの分類の一つである。

数学において最も基本的と見なされる代数的構造の一つであり、数学や物理学全般において、さまざまな構成に対する基礎的な枠組みを与えている。

群はそれ自体が研究対象であり、その領域は群論と呼ばれる。

定義

集合 G とその上の二項演算 μ の組 (G, μ) が群であるとは、以下の四つの条件を満たすことをいう。

閉性

G の元 g, h がどの組み合わせをとっても、μ(g, h) がまた G の元である。

(
∀
g
,
h
∈
G
)
{\displaystyle (\forall g,h\in G)}
[
μ
(
g
,
h
)
∈
G
]
{\displaystyle [\mu (g,h)\in G]}

結合法則

G の元 g, h, k がどの組み合わせをとっても、μ(g, μ(h, k)) = μ(μ(g, h), k) を満たす。

(
∀
g
,
h
,
k
∈
G
)
{\displaystyle (\forall g,h,k\in G)}
[
μ
(
g
,
μ
(
h
,
k
)

)

μ
(
μ
(
g
,
h
)
,
k
)
]
{\displaystyle [\mu (g,\mu (h,k))=\mu (\mu (g,h),k)]}

単位元の存在

G の元 g がどの値をとっても、μ(g, e) = μ(e, g) = g を満たす G の元 e（単位元）が存在する。

(
∃
e
∈
G
)
{\displaystyle (\exists e\in G)}
(
∀
g
∈
G
)
{\displaystyle (\forall g\in G)}
[
μ
(
g
,
e

)

μ
(
e
,
g

)

g
]
{\displaystyle [\mu (g,e)=\mu (e,g)=g]}

逆元の存在

G の元 g がどの値をとっても、μ(g, x) = μ(x, g) = e を満たす G の元 x が存在する。

(
∀
g
∈
G
)
{\displaystyle (\forall g\in G)}
(
∃
x
∈
G
)
{\displaystyle (\exists x\in G)}
[
μ
(
g
,
x

)

μ
(
x
,
g

)

e
]
{\displaystyle [\mu (g,x)=\mu (x,g)=e]}

このような x が存在すれば、x は g ごとに一意であり、この x を g の G における逆元という。

逆元はしばしば、g−1 あるいは演算を加法的に書く場合には − g と表される。

群より広い概念として、集合とその集合上で閉性を満たす二項演算の組をマグマ、結合法則を有するマグマを半群、単位元を有する半群をモノイドという。

また、交換法則を有する群をアーベル群または可換群という。

現代の標準的な群の定義は上述のようなものであり、公理は左右対称に書かれているが、これらは冗長であることが知られている。

例えば、結合法則と左単位元の存在と左逆元の存在だけを要請してもよい[1]。

あるいは、結合法則および左右の商が存在すること

(
∀
a
,
b
∈
G
)
{\displaystyle (\forall a,b\in G)}
(
∃
x
,
y
∈
G
)
{\displaystyle (\exists x,y\in G)}
[
a

x

b

y
a
]
{\displaystyle [ax=b=ya]}
を要請してもよい[1]。

また複雑な単一の公理により群を定義する方法もいくつか知られている[2]。

二項演算を（直積集合 G × G を定義域とする）写像として強調したい場合を除けば、g・h、または単に gh と書く場合が多い。

また、この演算を「積」や「乗法」と呼ぶことが多いが、加法と呼ばれている二項演算をもとにしてできる群もあるので、注意する必要がある。

さらに積が文脈から明らかなときには、群 (G, μ) のことを単に群 G と台集合を指定するだけで済ませることがほとんどである[3]。

概略

群の概念は、数学的対象 X から X への自己同型の集まりの満たす性質を代数的に抽象化することによって得られる。

この集まりは X の対称性を表現していると考えられ、結合法則・恒等変換の存在・逆変換の存在などがなりたっている。

集合論にもとづき X が集合として実現されている場合には、自己同型として X からそれ自身への全単射写像を考えることになるが、空間や対象の持つ構造に応じてさらに付加条件を課すことが多い。

例えば、ベクトル空間 X に対してその自己同型写像の集まりを考えると群が得られる。

また、平面上に正三角形など何らかの対称性を持った図形が与えられているとき、平面全体の変換のうちでその図形を保つようなものだけを考えることによって、図形の対称性を表す群を取り出すことができる。

例

集合 {1, 2, …, n} の上の置換（全単射）全体は、写像の合成を二項演算とし、単位元を恒等写像、逆元を逆写像とすることで群になる。

この群を n 次の対称群といい、Sn と表記する。

整数、有理数、実数、複素数の各集合は全て、算術的加法と群を成す。

なお、可換なのでその群はアーベル群である。

0を除く有理数、0を除く実数、0を除く複素数の各集合は全て、算術的乗法と群を成す。

なお、可換なのでその群はアーベル群である。

算術的乗法に対する逆元は算術的除法によって与えられるため、0を台集合に含めて群を成すことはできない。

四元数から 0 を除いたものは乗法に関して非可換群を成す。

群を成す超複素数系は四元数までであり、結合法則を満たさない八元数は群を成さない。
（実数係数の）n 次正則行列全体の集合はどの行列も逆行列を持つから群になる。

この群のことを GLn(R) と表し、n 次の実一般線型群と呼ぶ。

さらに行列式が 1 であるという条件を課したものも群を成す。この群を SLn(R) と書き、n 次の実特殊線型群と呼ぶ。

n 次直交行列全体も群を成す。

この群を On と書き、直交群と呼ぶ。

これは、n 次元ユークリッド空間において、長さを変えないような変換全体の成す群である。

直交行列の行列式は ±1 である。

行列式が 1 であるような直交行列全体からなる群を SOn と書き、特殊直交群と呼ぶ。

複素数係数の行列に対しても同様な群が定義できる；

その時、直交行列の類似物としてユニタリ行列を考える。

直交群に対応するものはユニタリ群 Un であり、特殊直交群の類似物は特殊ユニタリ群 SUn になる。

正則行列による群の構成はベクトル空間の自己同型写像による群の構成の特別な場合だと見なすことができる。

ベクトル空間 V 上の可逆線型変換全体 GL(V) は V のベクトル空間としての対称性を表していると考えられるが、これは V 上の一般線型群と呼ばれる。

V に付加的な構造を与えることでその対称性は変わり、例えばベクトルの長さを定める計量を保つような線型同型写像を考えることで（考えている計量に付随した）直交変換群が得られる。

T を座標平面の原点を重心とする正三角形とする。平面全体の等長変換のうちで T を保つものには、恒等変換、原点に関する120度、240度の回転と各頂点と対辺の中点を結ぶ軸を対称軸とする折り返しの6つがある。

これらによって T の対称性が表されていると考えることができる。

これら6つの変換の成す群は3次対称群あるいは位数6の二面体群と呼ばれる群に同型になる。

位数6の非可換群は同型の違いを除いて唯一であり、また、この群は位数最小の非可換群でもある。

楕円曲線は可換群の構造を持つことが知られている。

リー群（連続群）
ガリレイ変換
ローレンツ群
空間群
結晶点群
磁気空間群（シュブニコフ群）
磁気点群
灰色群

基本的な概念

位数

群 G の元の数（基数）を位数（英: order）という[3]。位数は集合に倣って |G| や #G などの記号で表される。位数が有限な群を有限群という。

部分群

群 G の空でない部分集合 H が G の群演算に関して閉じていて、H の任意の元に対して、逆元が H の元であるとき、この部分集合 H を G の部分群といい H ≤ G または G ≥ H と表す。

これは空でない部分集合 H の任意の元 a, b に対して ab−1 ∈ H が成り立つことと同値である[4]。

G が群であれば、G および {e}（単位元のみからなる群、単位群）は必ず G の部分群になる。

これらを自明な部分群という（単位元のみからなる部分群のみを指す場合もある）。

それ以外の部分群は、自明でない部分群あるいは真の部分群と呼ぶ（真部分集合であるような部分群という意味で、真の部分群に単位群を含める場合もある）。

部分群 N が群 G の任意の元 g に対して gNg−1 = N を満たすとき、N をGの正規部分群といい、
N
◃
G
{\displaystyle N\triangleleft G} または
G
▹
N
{\displaystyle G\triangleright N} と書く。

アーベル群 G の任意の部分群は正規部分群である。また、自明でない群 G が自身と自明な部分群しか正規部分群を持たないとき、G は単純群であるという。

剰余類・剰余群

部分群 H と G の元 g について、gH はある G の部分集合になる。

2 つの g, g’ について gH, g’H は全く一致するか交わらないかのいずれかである。

従って、

G

⨆
λ
∈
Λ
g
λ
H
{\displaystyle G=\bigsqcup {\lambda \in \Lambda }g{\lambda }H}
と非交和に書き表せる。

それぞれの gH を（H を法とする g の属する G の）剰余類（または傍系）という。

|gH| = |H| が成り立つので結局 |G| = |Λ||H| が成り立つ。

G が有限群ならばこれは H の位数が G の位数を割り切るということをいっている（ラグランジュの定理）。

特に素数位数の群は巡回群である。

|Λ| を [G : H] とか (G : H) などと書いて H の（G に対する）指数という。

指数 1 の部分群はもとの群であり、指数 2 の部分群は常に正規部分群である。

N を正規部分群とするとき gN = Ng が成り立つ。

すると、二つの剰余類 gN, hN について gN · hN = ghNN = ghN が成り立ち、剰余類の間に演算を定義することができる。

ここからすぐにこの剰余類全体は群を成すことが分かる。この群を G の N による剰余群または商群といい、G/N と表す。

群の準同型・同型

群 G1 から群 G2 への写像 f が任意の G1 の元 g, g’ について f(gg’ ) = f(g)f(g’ ) を満たすとき、f を準同型（写像）という。（G1 = G2のときは特に自己準同型という。）

さらに準同型 f が全単射であれば、f を同型（写像）という。G1 から G2 への同型が存在するとき、G1 と G2 は同型であるといい、

G
1
≃
G
2
{\displaystyle G_{1}\simeq G_{2}}　あるいは　
G
1
≅
G
2
{\displaystyle G_{1}\cong G_{2}}
と表す。2つの群 G1, G2 とその間の準同型写像 f: G1 → G2 に対し、準同型 f の核 Ker f は G1 の正規部分群である。このとき f の像 Im f は G を f の核 Ker f で割った剰余群に同型である：

G
1
/
K
e
r
f
≃
I
m
f
.
{\displaystyle G_{1}/\mathrm {Ker} \,f\simeq \mathrm {Im} \,f.}
これを（群の）準同型定理（特に第一同型定理）という。

群 G の自己同型（G から G への同型写像）全体の成す集合を Aut(G) と表すと、 Aut(G) は写像の合成を積として群となる。Aut(G) を G の自己同型群と呼ぶ。

群 G の任意の元 g に対し、写像 Ag: G → G を

Ag(x) = gxg−1 (for all x ∈ G)
で定めると、この写像は G の自己同型を定める。

この形で得られる自己同型を G の内部自己同型と呼び、G の内部自己同型全体の成す集合を Inn(G) と表す。

Inn(G) は Aut(G) の正規部分群であり、Inn(G) を G の内部自己同型群と呼ぶ。

さらに剰余群 Out(G) = Aut(G)/Inn(G) を外部自己同型群（英語版）とよび、その元を外部自己同型という。

群 G の部分群 N が正規部分群であることと、N が G の任意の内部自己同型で不変であることは同値である。さらに N が Aut(G) の作用で不変なら N は G の特性部分群であるという。

共役（※　キョウヤク）

群 G の二つの元 x, y に対し、y = Ag(x) = gxg−1 となる g ∈ G が存在するとき、x と y は互いに共役（共軛ともかく）であるという。

同様に、部分群 H, K に対し、H = gKg−1 となる g ∈ G が存在するなら、二つの部分群 H, K は互いに共役であるという。

共役であるという関係は群 G の同値関係である。

群 G を共役という同値関係で類別したときの同値類を共役類という。

有限群 G をその共役類 Cl1, …, Cln に類別すれば、位数に関して次の等式

|
G

|

∑
k
|
C
l
k
|
{\displaystyle |G|=\sum {k}|\mathrm {Cl} {k}|}
を考えることができる。これを類等式と呼ぶ。

G の元 x がその中心 Z(G) に属することと x の属する共役類が {x} なる一元集合であることとは（中心の定義から直ちにわかるように）同値であり、2 個以上の元からなる共役類の全体を C1, C2, …, Cr とすれば、類等式は

|
G

|

|
Z
(
G
)
|
+
∑

i

1
r
|
C
i
|
{\displaystyle |G|=|Z(G)|+\sum {i=1}^{r}|C{i}|}
の形に書くことができる。

有限群 G が p-群（位数が p の冪（※　ベキ）であるような群）ならば、その中心が自明群でないことは類等式から直ちにわかる。

中心・中心化群・正規化群

群 G のすべての元と可換な G の元の全体を Z(G) や C(G) などと書いて、G の中心という。群 G とその部分集合 S に対し、G の部分集合

C
G
(
S

)

{
g
∈
G
∣
s

g

g
s

(
∀
s
∈
S
)
}
{\displaystyle C_{G}(S)={g\in G\mid sg=gs\ (\forall s\in S)}}
は S をその中心に含む G の部分群となる。この群 CG(S) を S の G における中心化群という。

S が一元集合 {x} であるとき、CG({x}) を CG(x) と略記する。G の各元 x に対して、その中心化群 CG(x) の G に対する指数 [G : CG(x)] は x の属する共役類の位数に等しい。

群 G の部分集合 S に対して、G の部分集合

N
G
(
S

)

{
g
∈
G
∣
g
S
g
−

1

S
}
{\displaystyle N_{G}(S)={g\in G\mid gSg^{-1}=S}}
は（S が部分群でなくとも）G の部分群となる。この NG(S) を S の G における正規化群と呼ぶ。

H が群 G の部分群であるときは、その正規化群 NG(H) は H を含む。

また H は正規化群 NG(H) の正規部分群である。

これを、NG(H) は H を正規化 (normalize) するといい表す。

一般に G のふたつの部分群 H1, H2 に対し、H1 が H2 を正規化するとは、

h
H
2
h
−

1

H
2
{\displaystyle hH_{2}h^{-1}=H_{2}}
が H1 のどの h についても成立することを言う。

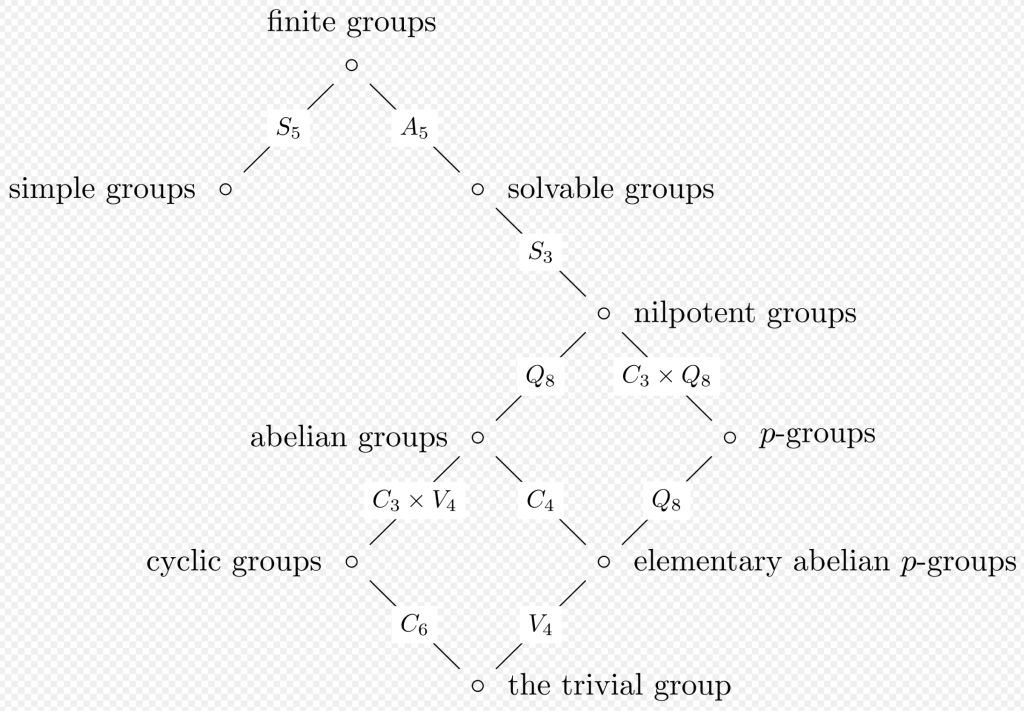
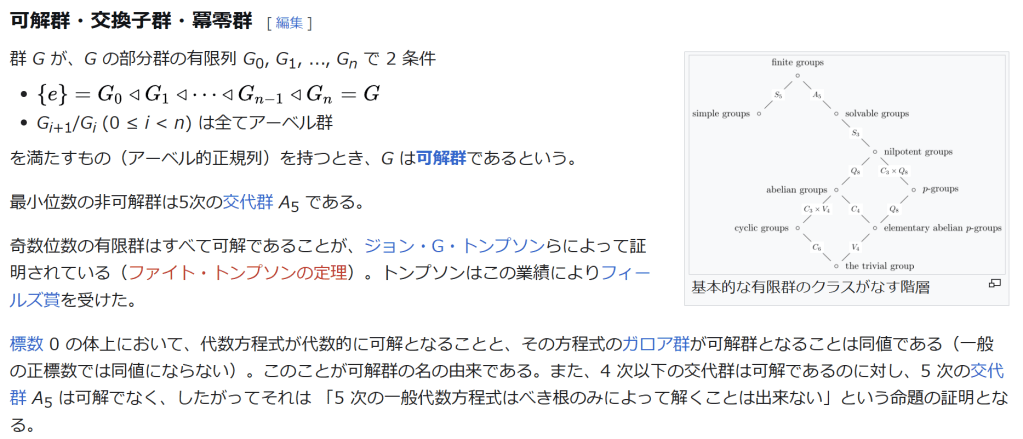
可解群・交換子群・冪零群

基本的な有限群のクラスがなす階層
群 G が、G の部分群の有限列 G0, G1, …, Gn で 2 条件

{
e

}

G
0
◃
G
1
◃
⋯
◃
G
n
−
1
◃
G

n

G
{\displaystyle {e}=G_{0}\triangleleft G_{1}\triangleleft \dotsb \triangleleft G_{n-1}\triangleleft G_{n}=G}
Gi+1/Gi (0 ≤ i < n) は全てアーベル群
を満たすもの（アーベル的正規列）を持つとき、G は可解群であるという。

最小位数の非可解群は5次の交代群 A5 である。

奇数位数の有限群はすべて可解であることが、ジョン・G・トンプソンらによって証明されている（ファイト・トンプソンの定理）。トンプソンはこの業績によりフィールズ賞を受けた。

標数 0 の体上において、代数方程式が代数的に可解となることと、その方程式のガロア群が可解群となることは同値である（一般の正標数では同値にならない）。

このことが可解群の名の由来である。

また、4 次以下の交代群は可解であるのに対し、5 次の交代群 A5 は可解でなく、したがってそれは「5 次の一般代数方程式はべき根のみによって解くことは出来ない」という命題の証明となる。

また、可解群の定義は次のように述べることもできる（上の定義と同値）：

G の部分群 D(G) を

D(G) = ⟨ xyx−1y−1 | x, y ∈ G ⟩
と定め、H1 = D(G), H2 = D(H1), … と帰納的に G の部分群 Hi を定めるとき、Hr = {e} となる自然数 r が存在するならば G を可解群と呼ぶ。

一般に、xyx−1y−1 を x と y の交換子と呼び、[x, y] であらわす。

さらに G の部分群 H, K に対し、[h, k] (h ∈ H, k ∈ K) の形の元で生成される G の部分群を [H, K] で表し、H と K の交換子群という。

この記号を用いれば、D(G) = [G, G] であり、これを G の交換子群と呼ぶ。

D(G) は G の特性部分群、したがって特に正規部分群である。

すぐに分かるように、D(G) = {e} は G がアーベル群となることに同値である。

したがって、剰余群 G/H がアーベル群となるなら H ⊇ D(G) であり、自然に G/H ⊆ G/D(G) と見なせるので、G/D(G) は G の剰余アーベル群の中で最大のものになる。

よって G/D(G) を G の最大剰余アーベル群あるいは G のアーベル化、アーベル商などと呼ぶ。

次の2つの同値な条件を満たす群を冪零群という。

Γ
1
(
G

)

[
G
,
G
]
{\displaystyle \Gamma _{1}(G)=[G,G]} とし、以下
Γ
i
+
1
(
G

)

[
G
,
Γ
i
(
G
)
]
{\displaystyle \Gamma {i+1}(G)=[G,\Gamma {i}(G)]} と定めるとき、ある r が存在して
Γ

r

{
e
}
{\displaystyle \Gamma _{r}={e}} となる。
G の部分群の列
{
e

}

G
0
<
G
1
<
⋯
<
G

n

G
{\displaystyle {e}=G_{0}<G_{1}<\cdots <G_{n}=G}
であって、各 Gi が G の正規部分群であり、Gi/Gi − 1 が G/Gi − 1 の中心に含まれるようなものが存在する。

可換群および有限 p 群はべき零群である。また、べき零群は可解群である。

可解性・べき零性の遺伝：べき零群の部分群および剰余群はべき零群である。可解群の部分群および剰余群は可解群である。逆に G の正規部分群 N と剰余群 G/N がともに可解群なら G は可解群である。（べき零群の場合には同様の主張は成り立たない。）

群の直積と半直積
群 G と群 H に対し、その直積集合 G × H 上に

(
g
1
,
h
1
)
(
g
2
,
h
2

)

(
g
1
g
2
,
h
1
h
2
)
{\displaystyle (g_{1},h_{1})(g_{2},h_{2})=(g_{1}g_{2},h_{1}h_{2})}
という積を定めることで群となる。これを群の（外部）直積または構成的直積という。また、群 G がその部分群 H1, H2 の（内部）直積である、あるいは直積に分解されるとは、以下の条件

H1 と H2 は G の部分群で G = H1H2 = {h1h2 | h1 ∈ H1, h2 ∈ H2} が成り立つ。
H1 ∩ H2 = {1G}, ただし 1G は G の単位元。
H1 の元と H2 の元は可換である。
がすべて満たされることをいう。

G

H
1
×
H
2
{\displaystyle G=H_{1}\times H_{2}}
で表す。右辺の直積を構成的直積と呼ぶこともある。

G の部分群という構造を落として、H1, H2 の外部直積をつくったものと内部直積とは、二つの自然な埋め込み

H
1
→
H
1
×
H
2
;

h
↦
(
h
,
1
g
)
,
{\displaystyle H_{1}\to H_{1}\times H_{2};\ h\mapsto (h,1_{g}),}
H
2
→
H
1
×
H
2
;

h
↦
(
1
g
,
h
)
{\displaystyle H_{2}\to H_{1}\times H_{2};\ h\mapsto (1_{g},h)}
をそれぞれ同一視することで本質的に同じものであることがわかる。

群 H と群 N と準同型写像 f: H → Aut(N) が与えられているとき、直積集合 N × H 上に

(
n
1
,
h
1
)
(
n
2
,
h
2

)

(
n
1
f
(
h
1
)
(
n
2
)
,
h
1
h
2
)
{\displaystyle (n_{1},h_{1})(n_{2},h_{2})=(n_{1}f(h_{1})(n_{2}),h_{1}h_{2})}
で積を定めると群となる。これを H と N の f による半直積といい、

G

N
⋊
H
{\displaystyle G=N\rtimes H}
で表す。なお、この群で N は正規部分群となる。群の拡大も参照。

有限群
→詳細は「有限群 § 主要な定理」を参照

有限アーベル群の基本定理
→詳細は「有限アーベル群の構造定理」を参照

G を有限可換群とすると、2以上の整数

e
1
|
e
2
|
⋯
|
e
n
{\displaystyle e_{1}|e_{2}|\cdots |e_{n}}
が存在して、G は

G
≅
Z
/
e
1
Z
×
⋯
×
Z
/
e
n
Z
{\displaystyle G\cong \mathbb {Z} /e_{1}\mathbb {Z} \times \cdots \times \mathbb {Z} /e_{n}\mathbb {Z} }
と巡回群の直積に分解する。このような ei たちは一意的に定まる。

また、素数 p1, …, pr（重複してもよい）と、正の整数 a1, …, ar が存在して、

G
≅
Z
/
p
1
a
1
Z
×
⋯
×
Z
/
p
r
a
r
Z
{\displaystyle G\cong \mathbb {Z} /p_{1}^{a_{1}}\mathbb {Z} \times \cdots \times \mathbb {Z} /p_{r}^{a_{r}}\mathbb {Z} }
と素数べき位数の巡回群の直積に分解する。

このとき、
p
1
a
1
,
p
2
a
2
,
⋯
,
p
r
a
r
{\displaystyle {p_{1}^{a_{1}},p_{2}^{a_{2}},\cdots ,p_{r}^{a_{r}}}} は順序の差を除き一意的に定まる。

コーシーの定理
→詳細は「コーシーの定理 (群論)」を参照

有限群 G の位数 |G| の素因数を p とするとき、位数 p をもつ G の元が存在する[5]。
シローの定理
→詳細は「シローの定理」を参照

素数 p が与えられているとき、有限群 G の位数を |G| = pam （ただし m は p と互いに素）と表す。このとき位数 pa の G の部分群を p-シロー部分群という。p-シロー部分群について以下が成り立つ[6]。

G のどの p-部分群も、ある位数 pa の部分群に含まれる。特に p-シロー部分群は存在する

相異なる p-シロー部分群の個数 np は p を法として 1 と合同である： np ≡ 1 mod p
任意の p-シロー部分群は G 内で互いに共役である

シューア・ツァッセンハウスの定理
→詳細は「シューア–ツァッセンハウスの定理（英語版）」を参照

N を有限群 G の正規部分群とし、|N| と |G:N| が互いに素であるとき、G の部分群 C が存在して、G は N と C の半直積となる。

バーンサイドの paqb 定理

p, q を素数とするとき、位数 paqb の有限群は可解である[7]。

有限べき零群の構造定理

有限べき零群はそのシロー部分群の直積に同型である[8]。

歴史

群の概念が初めてはっきりと取り出されたのは、エヴァリスト・ガロアによる根の置換群を用いた代数方程式の研究だとされている。

16世紀中頃に、ジェロラモ・カルダーノ、ルドヴィコ・フェラーリらによって四次方程式までは冪根による解の公式が得られていたが、5 次以上の方程式に解の公式が存在するのかどうかはわかっていなかった。

その後18世紀後半になってラグランジュによって代数方程式の解法が根の置換と関係していることが見出された。（「ラグランジュの定理」にその名が残っているのはこのためである。）

19世紀に入り、ルフィニやニールス・アーベルによって五次以上の方程式にはべき根による解の公式が存在しないことが示された。

ガロアは、より一般に任意の代数方程式について根が方程式の係数から加減乗除や冪根の操作によって得られるかどうかという問題を、方程式のガロア群の可解性という性質に帰着した。

ガロアの研究に端を発する群を用いた代数方程式の理論は今ではガロア理論と呼ばれている。

ガロア理論によれば五次以上の代数方程式の非可解性は交代群が単純であることによって説明される。

このような有限単純群の分類は20世紀に大きく発展し、1980年代までにいくつかの系列と26の例外からなる有限単純群の同型類のリストアップが完成した。

特殊な応用例

抽象的な群の概念を考えることによって古典的な数学の対象とは異なるものに群の言葉を導入することができるようになる。

文化人類学に群の理論が応用された例として、アンドレ・ヴェイユによるムルンギン族の婚姻体系の解析が挙げられる。

オーストラリア・アボリジニのムルンギン族は独特の婚姻体系を持っており、結婚が許される間柄や許されない間柄を定める規則が西洋や日本のものとは全く異なっていた。

文化人類学の研究では婚姻関係の規則を列挙して述べるのが普通だったが、ムルンギン族の体系は厳密だがとても複雑なもので、そうした手法による理解は困難に思われた。

1945年にクロード・レヴィ＝ストロースからこの話を聞いたアンドレ・ヴェイユは、許される婚姻の型を決定する規則が群をなしていることなどを発見し、群論を活用してその体系を解明した。

出典

[脚注の使い方]

^ a b バーコフ & マクレーン 1967, 第VI章 4. 抽象群.
^ McCune, W.W. (1993), “Single axioms for groups and Abelian groups with various operations”, Journal of Automated Reasoning 10: 1–13, doi:10.1007/BF00881862
^ a b Robinson 1996, p. 2
^ Robinson 1996, 1.3.1 (The Subgroup Criterion).
^ Robinson 1996, 1.6.17 (Cauchy’s Theorem).
^ Robinson 1996, 1.6.16 (Sylow’s Theorem).
^ Doerk & Hawkes 1992, p. 210.
^ Robinson 1996, 5.2.4.

参考文献

ガーレット・バーコフ、ソンダース・マクレーン『現代代数学概論』（改訂3版）白水社、1967年。NDLJP:2422244。
Doerk, Klaus; Hawkes, Trevor (1992). Finite soluble groups. de Gruyter Expositions in Mathematics. 4. Walter de Gruyter & Co. ISBN 3-11-012892-6. MR1169099. Zbl 0753.20001
Robinson, Derek J. S. (1996). A course in the theory of groups. Graduate Texts in Mathematics. 80 (Second ed.). Springer-Verlag. ISBN 0-387-94461-3. MR1357169. Zbl 0836.20001

群 (数学)

)

)

)

)

)

x

b

G

|

|

i

)

g

)

1

1

}

n

)

)

r

}

n

)

G

)

G

共有: