【第11回】½+⅓=⅖ 〜分数ができない大人〜[前編](東京財団政策研究所ウェビナー)https://kyoikutsushin.jp/webiken/webiken11-01.html
※ まあ、この程度の「基盤」しかないところに、「ICT」とか、「情報理論」「コンピューター学」とかを、打ち立てようとしているわけだよ…。
※ それでも、「世界」の中では、「マシ」な方なんだと…。




『教職の制度設計全体が大転換を迫られている。員数の確保策はもちろん、教員の質担保も問題になる。その一方、子どもたちはそこでどう学んでいるか、学び続けているのかに目を凝らすと、奇妙な実態が浮かんでくる。
それが「分数ができない大人」の存在だ。「分数ができない大学生」が社会に衝撃を与えたのは一九九〇年代。それから三〇年以上たち、「分数ができない大人」が社会を担っている現状は何を物語るのだろうか。産業界、大学、教育行政の識者たちと一緒に考える。
司会:松本美奈 ジャーナリスト、一般社団法人Qラボ代表理事、東京財団政策研究所研究主幹
[前編][後編]
登壇者
井出隆安氏
1946年長野県生まれ。
前杉並区教育長、杉並区立久我山小学校長、東京都教育庁指導部長、
同人事企画担当部長などを歴任。
牛瀧文宏氏
1962年兵庫県生まれ。
京都産業大学理学部教授・理学部学部長・大学院理学研究科長。
大平真吾氏
1963年東京都生まれ。食品メーカー人事総務部門本部長。
司会:松本美奈
1964年東京都生まれ。
東京財団政策研究所研究主幹
(「教職の制度設計を再構築する 量の確保・質の担保の視点から」プログラム研究代表)。
松本 「1/2+1/3=2/5~分数ができない大人~」へようこそ。司会の松本美奈です。本日は二部構成で進めます。前半を参加者からの発表、後半を皆さんとの異見交論に充てます。まずは本日のゲストのご紹介。一言コメントもお願いします。井出さん、牛瀧さん、大平さんの順でどうぞ。
井出 「分数ができない大人」は大変ショッキングです。学んでも使えないものに、中学から大学まで一〇年学んでも使い物にならない英語教育もあげられます。一方で、学校で勉強しているのに、例えばみそ汁が作れない、逆上がりができないということは、社会的問題になってない。なぜだろう、不思議です。今日はそんなことも踏まえて議論をしましょう。
牛瀧 日本は分数より小数の文化で、使わないから忘れてしまう。その程度のことかもしれません。ただ分数ができないということは、日常生活でそれほど不自由はないかもしないけれど、企業、生産者側の人の現状としては問題でしょう。ほかにも忘れてしまっていることがあるのではないか。それも気がかりです。
大平 従業員が六五〇名ほどいる食品メーカーで、二〇〇〇年から新卒の採用にかかわっております。私としては、分数に限った話ではないと思っています。できないことをそのままにして、「それで構わないや」という思考がまん延してしまっているのではないでしょうか。むしろ、そのことに危機感を覚えています。
松本 ではここから、問題提起・発表を始めます。
政策が小学校教員になる層を変えた
松本 では私から「分数ができない大人」を取り巻く現状について、問題提起をいたします。
学習指導要領で分数が出てくるのは小学校二年生です。それだけ長い時間学んでいるのだから、大人になってできないということは「本人の問題じゃない?」という疑問が出てきます。そうでしょうか。
本日のタイトル「分数ができない大人」は、一九九〇年代の名著『分数ができない大学生』を基底にしています。数学者や経済学者らが国公私立大学の学生対象に独自に行った学力調査を踏まえています。調査の結果、基礎科目全体の学力が低下している。しかも東大・京大の下位五〇%の学生の学力が深刻な状態と指摘しました。「分数ができない」はそうした現実を象徴する表現として使われています。
試験は、小学校・中学校レベルの基礎的な内容で、その結果から二つの課題が見つかりました。
まず、入試で数学を課されていない学生の点数が低かった。
もう一点は、国公立の教員養成課程の学生の点数が極めて低かったことです。
そのことについて、同書はこう指摘しています。「初等教育の教員志望者の中に初等的な数学ができない学生が多く存在することは、将来の日本の経済・技術の基盤を揺るがす問題だ」。分数ができない大人にしても、本人の問題に矮小化せず、政策的な課題とみるべきでしょう。これを子どもと教員の問題に分けて考えてみましょう。
まず子どもの問題としてみると、二つの疑問点が浮かびます。まず履修主義。できなくても四月になったら次の学年に上がれるシステムです。
もう一つは算数の時間数の減少です。学習指導要領で一九六八年と二〇一七年を比べてみると、約五〇年間で三六時間減っていました。
次に教員の問題です。大学入試・教職課程・採用試験、教員になってからの研修をみると、算数や数学を理解していなくても先生になれる、先生でいられる現実があることに気づかされます。
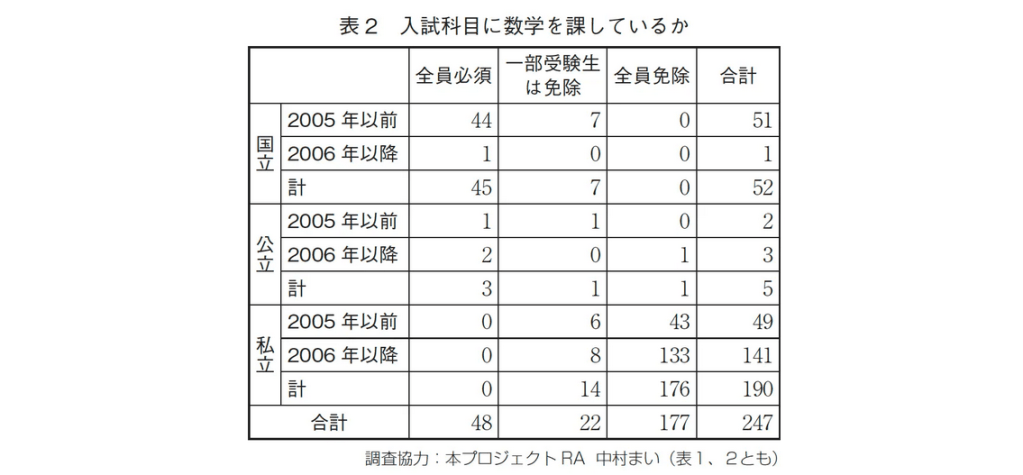
「分数ができない大学生」の時代と大きく変わったのが小学校教員を養成する大学です。当時は国立大学が中心でした。二〇〇六年度以降は私立大学が参入し、今や小学校教員の半数は私大出身です(表1)。
この流れは一九八〇年に始まっています。国立大学の教員養成学部定員の削減が続き、二〇〇四年度には国立大学が法人化。そして二〇〇六年度に小学校教員養成に関する規制を完全撤廃し、私大に全面的に門戸を開きます。
すでに少子化で、大学は受験生の争奪戦をしていました。小学校教員免許が取れることは、私立大学にとって「売り」です。でも入試に数学が課されていたら、受験生は来ない。そこで小学校教員養成の学部であっても、数学を課さないという選択をした。
私が研究代表を務める研究プロジェクト「教職の制度設計を再構築する」で調べたところ「数学全員必須」の私大は皆無でした(表2)。小学校教員になる層が変わった、政策が小学校教員になる層を変えたと言えるでしょう。さらに、大学に入って算数や数学をきちんと学ぶ時間もないのです。学生たちは、算数・数学を教えられるほど学んでいないことになります。
「名前を書けば筆記合格」が八割
教員採用倍率はどうなのか。教員採用倍率は低迷しています。中でも問題なのは、一次、筆記試験の倍率で、八割の自治体が一倍台でした。名前を書けば合格するレベルです。
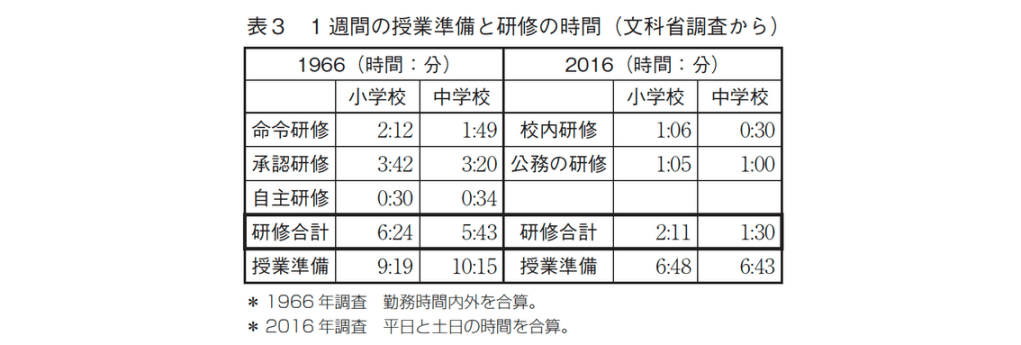
教員になった後、研修で学んでくれればいいのですが、研修時間そのものがこの五〇年間で三分の一に減っています(表3)。
文科省は「学び続ける先生」を唱えていますが、現実は厳しいでしょう。日本の公教育を担う教員の質は、大学入試と教員採用試験、採用後研修で担保されてきたとされています。しかし現状を見ると、どれもが危機的状況です。
今、政府は理系人材、デジタル人材の確保に躍起です。その人材を育てる教員がこの状態でどうやって育つのか。「分数ができない大学生」が指摘した問題点が、じわじわとボディーブローのように効いています。
「分数ができない大人」は、政策の問題です。「分数ができない大学生」を「分数ができない大人」のままに社会に送り出してしまった。
「生まれてきてよかった」、「学ぶって楽しい」と子どもたちが思える日本にしたい。それが私たちの研究プロジェクト、このセミナーが狙うところです。子どもたちが学ぶ環境、支援を見直さなくてはいけない時期にきています。「分数ができない大人」の存在がそのための警鐘を鳴らしています。
次に大平さんに、食品メーカーで人事を総括している立場から問題提起をお願いします。
「パーセンテージがわからない」社員に悲鳴
大平 当社の新卒採用の例を通して、現状を報告します。
高校三年生の採用選考です。高校生の採用は大学生と異なり、直接生徒と企業側が接触できない立て付けです。求人の際には、高校の進路指導の先生を訪ねて、最近の高校生の様子を伺う機会が多いです。先生方の話で、「分数やパーセンテージが苦手な生徒が多い」と聞かされるようになったのは二〇〇四年、二〇〇五年ぐらいと記憶しています。
採用選考にあたっては、生徒の学業成績などを全国統一の書面にまとめ、提出していただきますので、そこである程度成績を確認して、それほど大きな問題はなかろうと判断し、採用を決めていました。
当社は三つの工場を違う地域に持ち、工場単位で求人をします。ある工場で高校生の採用面接をしているときに、ふと「1/2+1/3っていくつ?」と尋ねたところ、正答率が三割程度しかなかったのです。翌年以降もその工場で同じ質問をしたところ、正答率は変わりませんでした。その後、他の工場からも「新入社員が分数を分かっていない」と指摘されました。食品メーカーでこれは非常に困る話ですが、「パーセンテージを理解できていない」という悲鳴も寄せられてきました。
図1
そこで二〇一一年から、学校から出てくる調査書だけでなく、社として算数と国語の筆記試験を始めました。これはその一例です(図1)。制限時間は三〇分。高校の先生には、事前に「小数と分数とパーセンテージの問題は必ず出します」と伝えています。「勉強させてくださいね」ということです。その年は三人の社員を採用しました。
ある生徒の学校での成績は「数学Ⅰ」「数学Ⅱ」「数学A」とも上々でした。ところが、当社の試験では一〇〇点満点の三〇点。小数の掛け算・割り算、それから分数の引き算がうまくできていなかった。パーセンテージに関する問題も解けませんでした。
二人目の生徒も、学校での数学の成績はよかったのですが、やっぱり三〇点でした。小数はできた問題もありましたが、分数は解答できなかったようです。最も問題なのはパーセンテージです。「濃度五%の食塩水三〇〇gに何gの食塩が入っていますか?」。この生徒は「一五〇g」と書いてきました。感覚的に「おかしくないかな?」とつかめないところに大変不安を感じました。この判断基準で食品を作られると大変なことになってしまうからです。
それから三人目の生徒は数学が得意で、二年次の数学の成績は「五」。ただし、実際にテストをしてみると、いろいろと取りこぼしがあることが分かります。
これは一例で、高校での数学の成績が「五」「四」でも、小数や分数の問題でつまずいている人は珍しくありません。この一〇年ほどこうした傾向が続いているとお考えください。
「分数ができない大人」ができるのは「作業」
さて、分数ができない人を採用して大丈夫なのか、とご懸念になるでしょう。メーカーでは製造現場は全て数字で管理をしています。原材料管理、生産量、製品の品質の管理・検査等々全て数字です。小数や分数、あるいはパーセンテージが理解できない社員でも、こちらからの指示を工夫すれば、作業は可能です。
例えば水分の含有率を厳格に管理しなければいけない製品二トンを作るとします。水分の含有率は五五・〇〇%にしなければいけない。では水の量はどれだけ必要か。
実際に製造するときは、水分を少なめで作って水分量を測定し、足りない分だけ水をつぎ足して完成させるという作業をします。そこで、分数やパーセンテージを理解できない社員には、「あと七三・四〇㎏水を足してください」と指示を出すことになります。
ただ、これは「作業ができる」という話で、生産管理や業務効率に関する仕事に深く関わらせることは難しいでしょう。
最近は、こちらの理解を超えるような発言を耳にします。
「原価計算って関係あるんですか?」と発言した社員がいました。入社三年で「バリスタになりたい」と言って退職しましたが、飲食業を経営する場合に原価率の計算は不可欠なのでどうしているのだろうかと心配になります。
「西暦って何ですか?」と聞かれることもあります。「今年が二〇二三年」とは理解していますが、「二〇二三年は令和何年?」といった西暦と和暦の関係が難しいというケースも、ここ二、三年で目にしています。
もちろん高校生だけの話ではありません。大学生の採用でも、社名を誤ったり、自宅の住所の郵便番号を宛先に書き込んだり、『宛』を消して『様』に書き換えることもできない。
自分で確かめる、考えることができない学生も現れています。
つまり、「できなくても自分はOK」と思っているのではないか、学ぶことから逃げているのではないか、とみています。幼い頃から消費者として承認されて生きてきたことで、これでいいと自信を持っているのかもしれません。学びから逃避していないにしても、「コスパ良く学ぶ」とか、「それを勉強すると自分にどんなメリットがあるんですか?」と大学生は日常的に口にしているようです。
ですから、当社では入社式直後の研修一時間目にはこう伝えています。「新入社員は無能な存在だよ」。何ができないかすら知らない「無意識無能」を、注意してもうまくできない「意識無能」、注意すればできる「意識有能」、さらに無意識に頭と体が動く「無意識有能」に成長させる。こうした学びのサイクルは一生続くと伝え続けています。私からは以上です。
松本 ありがとうございました。続いて牛瀧さんです。数学の教科書作成や、近畿・東海・中国地方を中心に現役教員の研修に携わり、大学生を指導されているお立場からご発言いただきます。
「割合がわからない」子どもたち
牛瀧 私は数学者の端くれですが、小中連携をきっかけに教育にかかわる機会をいただいてきた者です。数学者は、非常に疑り深い人間です。今日のタイトルの「分数ができない」にしても、まず「ほんまかいな?」と考えるわけです。そこで平成二十七年度の全国学力調査(学テ)をもとに、小中学生は本当に分数ができないのかを考えました。最近のものでないのは、当時は算数・数学共にA・Bに分かれていて、Aは単純計算が出題されていてわかりやすいからです。
この問題の通過率を見ると「28+72」は九八・二%、「6.79-0.8」は六九・七%はできている。次の「5/9-1/4」、今日のタイトルの「1/2+1/3」よりよほど難しいけれども八一・五%できています。「5/6÷7」も八四・三%。他の年も合わせて全国の学力調査を見た限りでは、小学校六年生、中学校三年生ぐらいの段階では「計算はできる」と言っていいレベルでしょう。
小学校の先生方の指導が行き届いていると評価しています。先生方、結構忙しい中で一生懸命されていると思います。
じゃあ何が問題なのか。何か見落としていることはないか。こちらは令和四年の学テ、小学校六年生の問題をいくつかみていきましょう。
〈オレンジの果汁が二五%含まれている飲み物があります。飲み物の量をもとにしたときの、果汁の量の割合を分数で表しましょう。〉
これに対して、一〇〇%の内の二五%ですから「1/4」と答えているのが四五・五%でした。「25/100」と書いている人も二五・五%いて、これも正解とされています。となると合計で七割が正解です。これだけ見ると、できているように思えますが、25/100が1/4とすぐに変換できない点が気になります。これは、クォーターの感覚が育っていないということでしょう。
〈オレンジの果汁が四〇%含まれている飲み物があります。この飲み物一〇〇〇mlには、果汁が何ml入っていますか。答えを書きましょう。〉
一〇〇〇mlの中の四〇%は四〇〇mlであると正答できたのが六四・八%、少ないですね。で、驚いたのはこの次です。
〈りんごの果汁が二〇%含まれている飲み物が五〇〇mlあります。この飲み物を二人で等しく分けると、一人分は二五〇mlになります。二五〇mlの飲み物にふくまれている果汁の割合について、次のようにまとめます。 二五〇mlは五〇〇mlの1/2の量です。このとき( )〉
この空欄を埋めるため三つの選択肢が示され、どれかを選ぶように指示されます。
①飲み物の量が1/2になると、果汁の割合も1/2になります
②飲み物の量が1/2になると果汁の割合は二倍になります
③飲み物の量が1/2になっても果汁の割合は変わりません
この問題の正答率は二一・六%でした。約1/5です。ジュースを二つに分けても、果汁の割合は変わらない。果汁の割合、つまり味は変わらないと正しく認識しているのが二一・六%ということです。味が変わらないことは誰だって分かるんですが、それを算数の言葉、数学の言葉に直せないのがこんなにいると理解したらいいと思います。
一番多い誤答が①で六七・七%、飲み物の量が1/2になると果汁の割合も1/2になると考えてしまったのです。先ほどの大平さんのお話とも関係してくると思います。
一体何が起きているか。操作的なことはできてもそこから先に課題があるのではないか。先程の話にありますように、割合の理解が進んでいない、これは問題です。「分数ができない」の意味はここにあるのではないでしょうか。割合は中学校では勉強しませんが、中学校でも学ばせたらいいと思います。小学校で学んでいない割合の処理や比の使い方などたくさんありますし。
AIドリルがメタ認知の力を奪う?
何に注意して子どもたちの学びを支えたらいいのか。計算できることは大切ですが、それでよしとせず、複合的にとらえられるようにすることが必要です。数学者の立場から言いますと、算数とか数学は「目に見えないことを見るための言葉」です。その数値によって物を理解することによって、例えば危険を回避することもできるわけです。ここに含まれている有毒ガスのパーセンテージがいくらだって書かれていたら、体験しなくてもその数値で危険度がわかるわけです。その数値の重要性、これを教えてくれるのが、算数や数学です。
私の専門で考えますと、私は三次元を超える、N次元の空間を日常的に考えているわけですけども、そういう目に見えない物であったとしても、数学の言葉で理解できるようになるものなんです。数学者の発想からするとそういうところは非常に重要だと思います。先ほどから話に出ている「割合」も目に見えません。リンゴ果汁四〇%だからと言っても目に見えませんし、そのことを利用するには想像力が必要になってきます。
割合に不安があると、生産者をはじめとして、職業人としてはやっぱり難しいですね。これは先ほどご指摘いただいたとおりかと思います。確かに計算練習は大切ですが、計算の大切さの意味は小学校算数と高校の数学では異なります。計算における意味は、高校の数学ではかなり大きいです。計算することによっていろんなことが分かってくるようになるので、計算を重視してもいいかと思います。しかし、今回の分数のような場合には意味を理解させ、自分の言葉として使いこなしていくことに重点を置いていただきたい。
さて、こういうことに基づいて提言します。数学者の端くれが言っていることだという程度に受け止めてくださったら結構です。
小学校の低学年は二年生を大切にすべきです。算数は二年生から学習時間が増えるんですが、ここを大切にしないといけません。二年生は九九が出てくる学年です。三年生から目に見えない物を扱うようになります。例えば小数、分数なんかも学習するんですね。四年生になると、面積のように計算によって初めて分かるような量が出てきます。そのことを教員もきちんと意識しておかなくてはいけません。教科担任制の必要性が言われていますが、私は複数教科担任制を提言します。例えば小学校五年生では算数と社会。小五の社会科はかなり統計が入ってくるので、この二つを両方ともできるような先生がほしいです。
教員研修によく参加しますが、指導法に偏らないで教科教育の視点を入れてほしいと思います。指導主事研修も必要かもしれません。
中学校の数学は、二年生と三年生の区切りで考える。これは重要なことです。中学校二年生までの数学は算数との連続性が強いですが、中学校三年生の数学は高等学校の内容と親和性があるからです。それは小中一貫教育の充実や高等学校でドロップアウトしない生徒の育成につながると思います。
最後にICTの活用について話します。ICTで学習活動が広がるのはいいことですが、危惧もあります。AIドリルです。
AIがその子の「できないもの」を勝手にいろいろと判断していることに注意をしてください。スキル向上にはいいかもしれませんが、メタ認知力が下手に使うと損なわれるのではないか、と危惧しております。
「メタ認知能力」と言いますと、「私はこれができた」「これができなかった」ということを振り返って、自分を見つめることができる力です。こういう力は子どもの自己成長力につながると思うのですが、自分で振り返る前に、機械がどんどんと、その子にできないものを与えていってくれる。
日頃ネットショッピングをしていると「あなたにおすすめ」って出てきますね。自分がこれが好きかどうか分からないのに、AIはどんどん与えてくれる。もしそれを簡単に受け入れたら、思考停止や思考放棄になる。一度でも受け入れたものが自分にぴったりで、「おすすめ」に任せればいいやとなったら依存症になる。
AIドリルが、その子に合ったものを教えてくれるのは便利ですけれども、子ども自身が自分の学びをメタ認知して、自己成長力を担保できるようにする工夫とセットで考えるべきかと思います。
こういうこともICTを使えばうまくできるので、上手に活用してほしいと思います。私からは以上です。ご清聴ありがとうございます。
松本 ありがとうございました。最後に井出さんです。小学校の先生、その後は東京都教育庁で人事に携わり、杉並区教育長としてユニークな政策を打ち出してきました。その立場からお願いいたします。
一億総劣化時代
井出 先ほど松本さんが「小学校の先生になる層が変わった」と指摘していました。そのあたりを踏まえながら話をします。「風が吹けば桶屋がもうかる」式の論理の飛躍がたまに出てきましたら、それは議論の中で間を埋めていくなり、あるいは質問に答えながら修正していきたいと思います。
タイトルは「『でも・なら』先生の時代がやってきた?」です。杉並区教育長の頃、「一億総劣化社会がやってきた」という話をしたことがあります。社会のあらゆるシステムが劣化しています。学校がちゃんと子どもを教えていて、そこでの学びは役に立っているのか。もしかしたら学校の教育機能も劣化しているのではないのか。学校を含めて一億総劣化社会の時代になったのではないかと考えたからです。この言葉は評論家の大宅壮一が、日本にテレビが入ってきたときに「こんな物が各家庭に行き渡ったら、日本は一億総白痴化する」と指摘していたことをもじったものです。
学校の教育機能、学校の教育力が低下してきているとしたら、それはなぜだ? 先生の質が下がってきたからか。ではなぜ先生の質が下がってきたのか。先生になる人がだいぶ変わってきたからなのか……。こうした問題を考えていきます。
はじめにおさらいです。先ほどの松本さんが、国立大学の小学校教員養成課程の定数が削減されたことを報告していました。一方で私立大学に対する規制が緩和され、二〇〇五年に五〇校しかなかった私立大学の教員養成課程が、二〇二〇年には一九〇校に増えたという内容です。その結果、小学校の教員になる層が変わってきたという指摘がありました。
小学校の先生には幅広い教養が求められます。そのため教育学部の履修内容はかなり幅が広くて、総合的な知の体系を広く薄く学ぶ構成になっているともいえるでしょう。算数、国語、理科、社会、音楽、図工、体育、道徳も特別活動もと、学校教育に登場してくるあらゆる場面を想定した教科領域があるわけですが、「広く浅く」というと語弊がありますので、「幅広い知識・教養」と言った方がいいかもしれません。
なぜ幅広い知識・教養が必要か。小学校の段階の子どもたちの理解や認識能力は未分化な状態です。中学・高校・大学のように専門に特化して、そこを掘り下げていくのとは違う学びが必要です。
小学校一・二年生の生活科を想定していただければ分かりやすいでしょう。日常生活の中で出会う「なぜだろう」「不思議だな」「どうしてこういうことが起きるんだろう」といった事象を、理科や社会科の定義や法則を適用して教えるのではなくて、事実から遡って考えていきます。
子どもたちの様々な疑問や問いかけに応え、考えを深めていく過程を支援するためには先生はいろんな知識を持っていないと困るんですね。
そういう意味では幅広く学んできてほしいけれども、現実は教養がない、常識が少し足らない先生が増えているようです。ここでいう「常識」とは、先生としての基礎的な教養と考えていただければいいです。
以前、新任教員を対象にした研修会で「考えるということはどういうことか」という話をした折に、「われ思う、故にわれあり」というデカルトの言葉をあげて、「これは誰の言葉か知っている人はいますか?」と聞いたところ、一〇〇人近くいた中で知っていた教員はわずかに二人でした。デカルトという名前が出てこないのですから、「方法序説」なんて縁のない話です。
ほかのことなら知っているかと思って、二本の平行直線が交わるという話をしたら、教員たちはみんな不思議な顔をしているんです。平行直線の定義を言わせればちゃんと答えられるけれども、交わる平行直線の話になると、もうちんぷんかんぷん。「何の話をしているんだろう?」という顔をするのです。
そこで地球儀を示して、どこで交わっているかを見せました。北極と南極で交わっています。平らな地図の上では交わらない経線が全部、北極と南極で交わっている。非ユークリッド幾何をちょっとでもかじっていれば、大学の一般教養の数学なり教職課程の講座なりで、そういうところを少しでも学んでいれば、「あ、あれですよね」って気づきますが、全く初めて聞いたという顔をされると、おっとっとってなるんですね。
ゼノンのパラドックスの話をしたこともあります。アキレスが亀に追いつけない話です。亀は歩みののろいものの象徴で、アキレスは速く走る象徴です。アキレスが前方にいる亀を追いかけるのですが、アキレスがはじめに亀のいたところに追いついたときには、亀はわずかに前進しています。ふたたびアキレスが追いかけて亀がいたところに追いついたときには、さらに亀はわずかに前進しています。アキレスが亀に追いつけるでしょうかという問題です。
小学校六年生を担任しているときにこの問題を出したらバッと手を上げて「先生、旅人算でしょ」って言った子がいました。「旅人算」は一定の方向に動く二つのものの隔たりの推移に関する問題です。「じゃあやってごらん」とその子に言いました。しばらくすると、その子は「先生、無理だ」って言うんです。「追いつかないよ、何回やっても」と。「そうだよね。これはね、インチキが一個挟まっているんだよ」と解説をしたら子どもたちも納得したようでした。
ところがこの話を新規採用の教員にしたときに、キョトンとした顔をしているんです。つまり、先生になる人たちの層が変わってきたっていうことの根底に、このあたりを大学で勉強してきてない現実がある。雑学の一部であったとしても、どこかで見たり聞いたりしてくるだけの暇もなかったのでしょうか。
今の先生は「大丈夫じゃない」
では、なぜそんな人が先生になっているのでしょうか。先生が足りないからです。採用試験も簡単にして、免許がなくても後から取ればいい。先生の資格を取っただけのペーパー・ティーチャーを「先生をやりませんか」と全部掘り起こす。試験の時期を大学三年次に前倒ししてかき集めようとするぐらい先生は足らなくなっている。われわれはそれを「どぶ板外して、どぶの底までさらわないと先生が見つからない」という悲鳴も耳にします。
そこで「でも・なら先生」の登場です。昔の「でも・しか先生」とは違います。教員養成系大学・学部は入りやすい。教員免許は取得しやすい。採用倍率が低くて合格しやすい。倍率の高い企業には入れないし、国家公務員にもなれないけれど、「先生なら」なれるという時代がやってきたようです。当然、先生の質、指導力は担保されているのか、先生は大丈夫かという疑問が起きます。結論から言うと、私は大丈夫じゃないと思っています。
大学での学びが、広く浅くどころか、狭く浅くになってくれば、当然学んでこなかったことも多くなるわけです。ましてや入試に数学がなければ、小学校・中学校で教えてもらったこと以上のものを身につけられないまま教員になってくる可能性もあるわけです。
では、大学で十分力を付けないまま教壇に立つことになった先生はどこで力をつけさせたらいいのか。教育委員会の立場からすると、先生になってから現場で力をつけてもらうしかありません。
現職教員のための研修機会は、制度化されたものや教育委員会が設定したものの他に、校内で行う研修や教員が学校を超えて組織する研究会などがあります。私は教員が組織する研究会の研修機能に期待しています。かつて職能団体としてのギルドが持っていた後進育成の仕組みです。学校が多忙化する中で、教え合ったり学び合ったりする先生の間の「同僚性」が薄れていると言われます。知識や経験が浅いまま教員になってきた人たちを「再教育」し、足らないところを補って力をつけていくためには同僚性の再生が不可欠です。
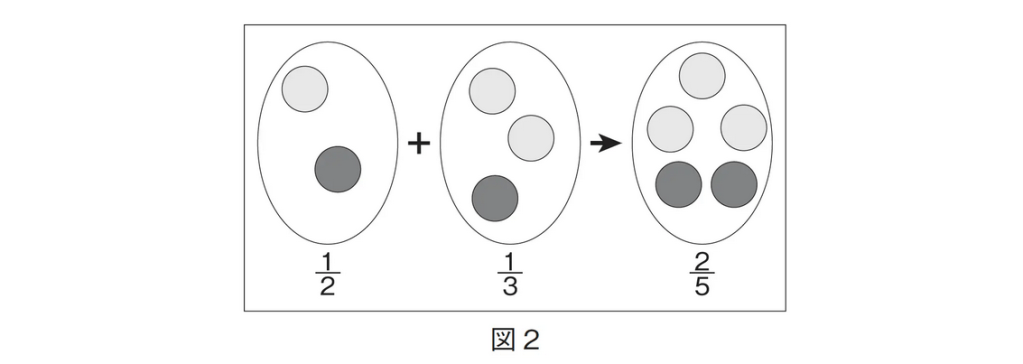
本日のタイトル「1/2+1/3=2/5」はもちろん正解ではありませんが、見方によっては間違っていないと考えることもできます。袋の中に緑とピンクの球が混在している状態を思い浮かべてください。一つの袋は一つずつ、もう一つの袋にはピンクが二つで、緑が一つ。「全部合わせると、緑は全体の何分のいくつ?」という問題だったらどうなりますか。それぞれの個数を足して「2+3」だから全体が五、そしてその中の緑は「1+1」で二個だから2/5になります(図2)。
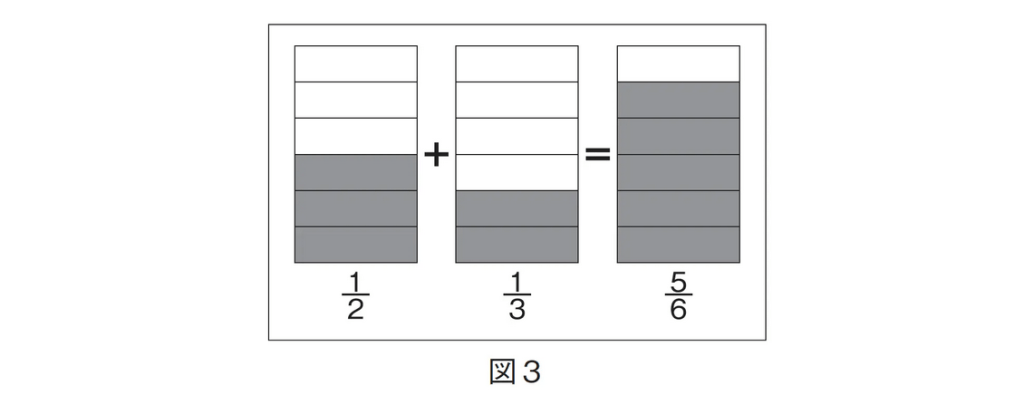
でもそれは「1/2+1/3=2/5」という計算が正しいということではありません。子どもの考えを取り上げて、どうしてそのように考えたのか問いかけて、なぜ合っていて、なぜ間違っているかを、行ったり来たりしながらわかりやすく説明することが、小学校の先生にできないと困ります。そういった事例は他にもあります(図3)。
こちらもご覧ください(図4)。
この計算ドリルは五問中三問正解ですから、通過率(正解率)は六割です。ところがよく見ていくとあることに気づきます。「12-7=5」、「13-8=5」、「11-6=5」は正解ですが、「17-9=2」、「15-9=4」は引く数から引かれる数の一の位の数を引いたのかもしれません。
そうであったすれば「12-7=5」、「13-8=5」、「11-6=5」も同じように計算して、結果的に正解になっただけかもしれません。繰り下がりのある計算の仕組みを理解しているか違う問題で確かめる必要があります。
実際にこのような極端な構成のテストをすることはありませんが、仮にこういう問題を出して結果だけを機械的に採点したら、一〇点満点の六点ということになります。
今朝のテレビで「先生が忙しいから誰かに採点させれば先生が忙しくなくなるでしょう」なんて言っていました。とんでもないことです。これは絶対に先生がやらなければいけないことです。指導と評価の一体化と言われるように、ここを見逃したら、繰り下がりの引き算の仕組みを理解しないまま先に行ってしまうことになります。誰かが代わりに採点すれば先生が楽になるという問題ではなくて、この部分だけは絶対に譲らない、ここはちゃんと分からせなきゃならないっていうところがあるということを分かる先生になってほしいと思います。
ひとこと
「分数ができない大人」の存在は、私たちに重い課題を突きつける。教員養成などの制度的な問題だけでなく、「わからないことを放置しても構わないという思考の蔓延」(大平氏)、「学校で勉強したのにできないことが他にもあるのに社会的問題になっていない」(井出氏)といった現実の深刻さを浮き彫りにするからだ。牛瀧氏はさらに、教育現場で広がるAIドリルが子どもの思考停止や思考放棄を助長するとも懸念する。
先日、経済産業大臣が話題のチャットGPTを国会答弁作成に使う可能性に言及していた。国家公務員の業務負担軽減を視野に入れているというが、日本の未来を議論する場に政治家も官僚も要らないと、自ら認めたように映る。「分数ができない大人」とどこが違うのだろう。
二〇〇六年に改正された教育基本法は前文で「我が国の未来を切り拓く教育」とうたいあげ、その目標に「幅広い知識と教養」「創造性」「自律の精神」を掲げた。頭を使わない、使えない大人が社会を担う現状は、AI任せの社会の未来の不気味さを予見し、胸を重苦しくする。(奈
みんなで異見交論前編
ページトップへ
トップページ
会社案内
出版案内
購入方法
お問い合わせ
授業ノート
授業ノートから
異見交論
異見交論(文部科学 教育通信 連載)
みんなで異見交論(WEBセミナー)
会社情報
個人情報保護方針
特定商取引法に関する法律に基づく表示
Q&A
Copyright THE EARTH KYOIKUSHINSHA Co., Ltd. All Rights Reserved. 』