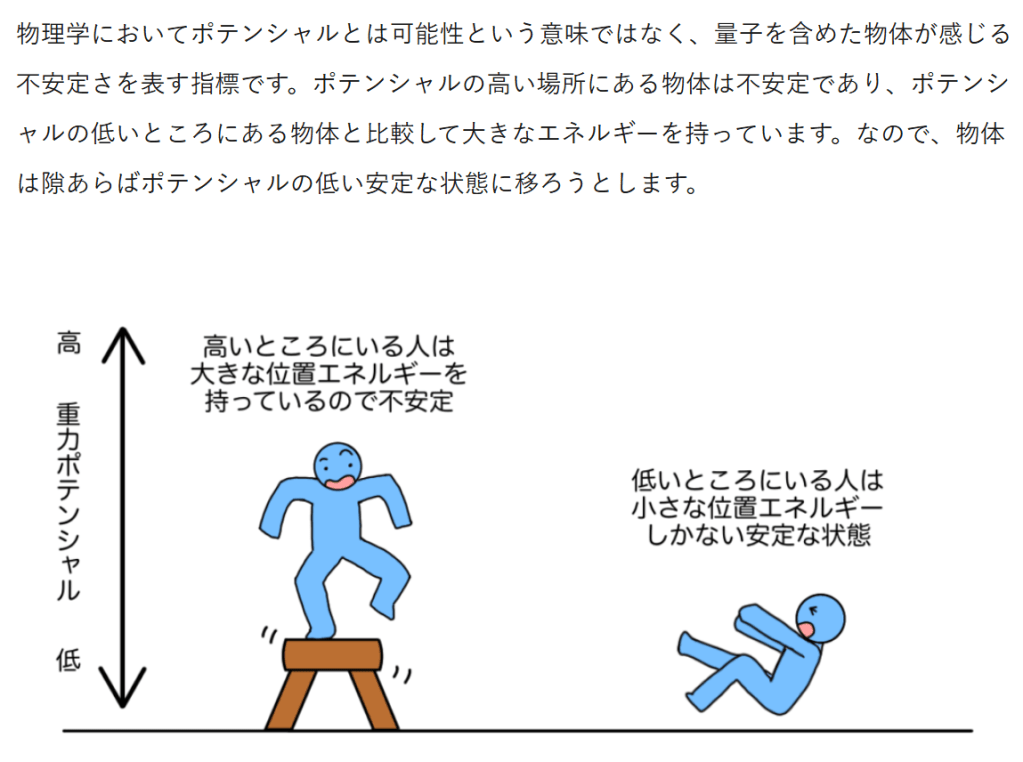
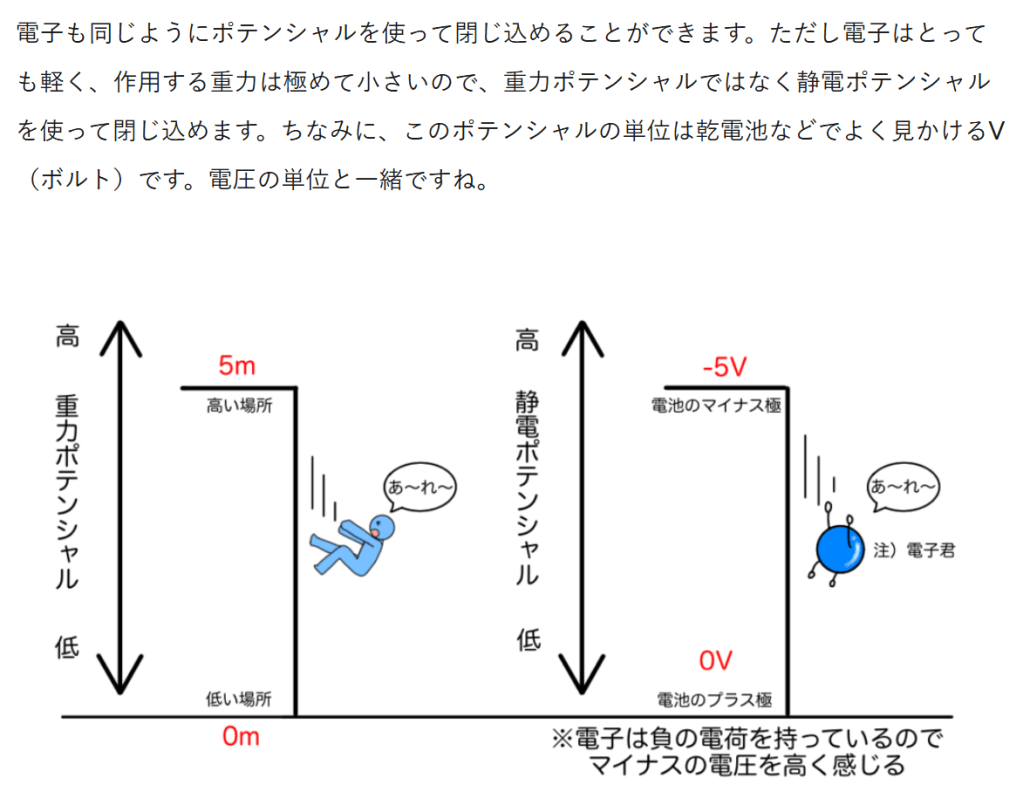
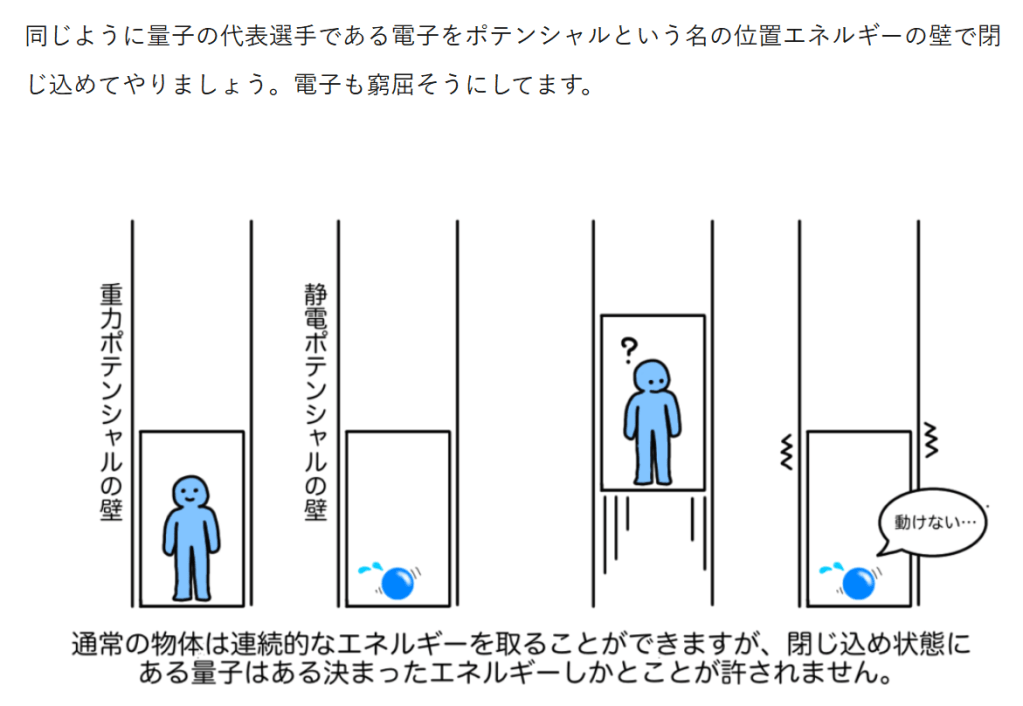
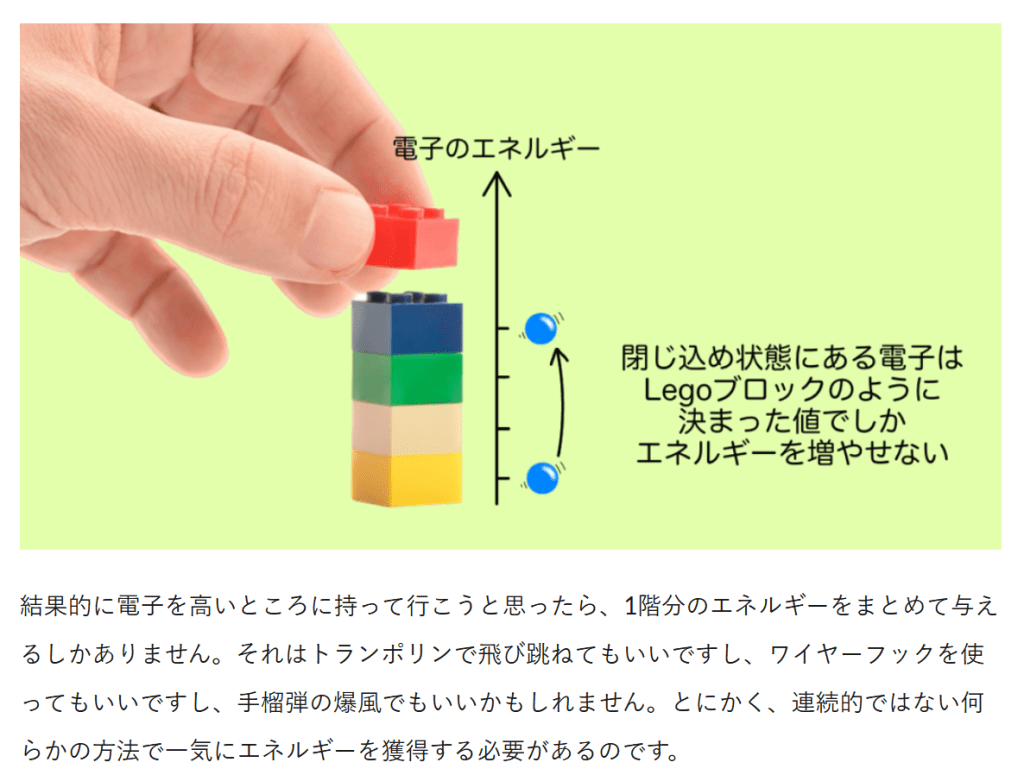
エネルギー保存の法則
https://ja.wikipedia.org/wiki/%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%E4%BF%9D%E5%AD%98%E3%81%AE%E6%B3%95%E5%89%87#:~:text=%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%E4%BF%9D%E5%AD%98%E3%81%AE%E6%B3%95%E5%89%87%EF%BC%88%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%E3%81%BB%E3%81%9E%E3%82%93%E3%81%AE%E3%81%BB%E3%81%86%E3%81%9D%E3%81%8F%E3%80%81%E8%8B%B1:%20law%20of%20the%20conservation%20of%20energy%EF%BC%89%E3%81%A8%E3%81%AF%E3%80%81%E3%80%8C%E5%AD%A4%E7%AB%8B%E7%B3%BB%E3%81%AE%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%E3%81%AE%E7%B7%8F%E9%87%8F%E3%81%AF%E5%A4%89%E5%8C%96%E3%81%97%E3%81%AA%E3%81%84%E3%80%8D%E3%81%A8%E3%81%84%E3%81%86%E7%89%A9%E7%90%86%E5%AD%A6%E3%81%AB%E3%81%8A%E3%81%91%E3%82%8B%E4%BF%9D%E5%AD%98%E5%89%87%E3%81%AE%E4%B8%80%E3%81%A4%E3%81%A7%E3%81%82%E3%82%8B%E3%80%82%E3%82%A8%E3%83%8D%E3%83%AB%E3%82%AE%E3%83%BC%E4%BF%9D%E5%AD%98%E5%89%87%E3%81%A8%E3%82%82%E5%91%BC%E3%81%B0%E3%82%8C%E3%82%8B%E3%80%82
『出典: フリー百科事典『ウィキペディア(Wikipedia)』
物理学
ウィキポータル 物理学
執筆依頼・加筆依頼
物理学
ウィキプロジェクト 物理学
カテゴリ 物理学
エネルギー保存の法則(エネルギーほぞんのほうそく、英: law of the conservation of energy)とは、「孤立系のエネルギーの総量は変化しない」という物理学における保存則の一つである。エネルギー保存則とも呼ばれる。
概要
→「熱力学第一法則」も参照
任意の異なる二つの状態について、それらのエネルギー総量の差がゼロであることをいう。
例えば、取り得る状態が全て分かっているとして、全部で 3 つの状態があったとき、それらの状態のエネルギーを A, B, C と表す。
エネルギー保存の法則が成り立つことは、それらの差について、
A − B = 0, B − C = 0, C − A = 0
が成り立っていることをいう。
時間が導入されている場合には、任意の時刻でエネルギー総量の時間変化量がゼロであることをいい、時間微分を用いて表現される。
エネルギー保存の法則は、物理学の様々な分野で扱われる。特に、熱力学におけるエネルギー保存の法則は熱力学第一法則 (英: first law of thermodynamics) と呼ばれ、熱力学の基本的な法則となっている。
熱力学第一法則は、熱力学において基本的な要請として認められるものであり、あるいは熱力学理論を構築する上で成立すべき定理の一つである。第一法則の成立を前提とする根拠は、一連の実験や観測事実のみに基づいており、この意味で第一法則はいわゆる経験則であるといえる。
一方でニュートン力学や量子力学など一般の力学において、エネルギー保存の法則は必ずしも前提とされない。
歴史
→詳細は「熱力学・統計力学の年表」および「熱の仕事当量」を参照
概要
この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: “エネルギー保存の法則” – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2012年12月)
ルネ・デカルトやゴットフリート・ライプニッツが、それぞれの仕方でこれを主張し、それぞれの支持者によって議論が長年に渡り行われた。
19世紀の中ごろ、ユリウス・ロベルト・フォン・マイヤー、ジェームズ・プレスコット・ジュール、ヘルマン・フォン・ヘルムホルツらによって、「力学的・熱・化学・電気・光などのエネルギーは、それぞれの形態に移り変わるが、エネルギーの総和は変化しない(保存される)」と主張された[1]。
20世紀にアルベルト・アインシュタインによって、質量とエネルギーの等価性という考え方が提唱され、別の形での保存が主張されたが、その有効性や有効範囲については、疑問視されることも多かった。
現在ではエネルギー保存の法則は、しばしば「最も基本的な物理法則の一つ」と考えられている。多くの物理学者が、自然はこの法則にしたがっているはずだ、と信じているのである。
活力論争
ルネ・デカルトは、1644年に出版した自身の著作『哲学の原理』(Principia Philosophiæ ) で[2]、宇宙においてquantitas motus(運動の量)の総和が保たれている、と主張した。
Deum esse primariam motus causam: et eandem semper motus quantitatem in niverso conservare.
— Principia philosophiae, Pars secunda, 36(デカルト『哲学の原理』第二章 36)
デカルトが主張した quantitas motus(quantity of motion, 運動の量)という概念は、現代の運動量とある程度似てはいるが、厳密には異なる概念である[3]。デカルトは「質量」という概念を持っていなかったし、デカルトは速度の大きさだけを重視し、向きが変わることについては考慮していなかった[3]。したがって、デカルトの quantitas motus を現代の運動量に対応する量と見なすことはできない。
ゴットフリート・ライプニッツは、運動の量というのを初めて数式で表現してみようと試みたが、デカルトとは異なって mv2 の総和が保存されている、と主張した。ライプニッツはこの量を vis viva(living force, 活力)と呼んだ。この vis viva という概念は、釣り合いなどの場面で想定される動きとしては見えない vis mortua(dead force, 潜在的な力)と対比しつつ置かれた概念である。
デカルトの考え方を支持する人々と、ライプニッツの考え方を支持する人々で議論が起こるようになった。これを「活力論争 (vis viva controversy)」という。議論は長年に渡って続いた。18世紀半ばになって、ジョゼフ=ルイ・ラグランジュやジャン・ル・ロン・ダランベールらが、両概念の明確化を試み、それらを区別したことによって、ようやく論争は沈静化した。
「エネルギー」の定義
1807年にトマス・ヤングは、vis viva という用語で表されていた運動の概念を、”energy” と呼んだ。energy はギリシア語の ἐνέργεια(羅: energeia, エネルゲイア)という語を基にした造語である。ギリシャ語のἐνέργεια (energeia ) というのは語の構成としては εν + εργον (en +ergon ) であり、εργον (ergon ) は「仕事」、εν— (en —) は「~の状態」という意味である。よって「仕事をしている状態」といったような意味である。アリストテレスの哲学において ἐνέργεια は、ものが持つ「可能態」の中から現実化された「現実態」を意味する。つまり、energy という用語を用いている背景には、眼には見えない「活力」が具体的な「仕事」に変化したのだ、という発想がある。
ヤングが energy という用語を用いたからといって、それが人々にすぐに用いられるようになったわけでもなく、人々の間に定着するようになったのは、あくまで後のことである。vis viva 相当の概念は、19世紀半ばでもしばしば、英語圏では “force” と呼ばれていたし、ドイツ語圏では „Kraft” と呼ばれていた。
現代的な意味で energy の語が用いられるようになったのは、ヤングより後のことで、1850年頃にウィリアム・トムソンによって kinetic energy(運動エネルギー)、1853年にウィリアム・ランキンによって potential energy(位置エネルギー)の語が定義された[4]。
19世紀前半のドイツ自然哲学
19世紀前半のドイツの自然哲学では、「破壊されることもなく、形態が様々に変換する根源的な何か」を „Kraft”(力)と呼んでいた。この自然哲学の概念は、現在の「エネルギー保存の法則」という概念の成立に大きな影響を与えている。
力学的仕事と熱に関する保存則の発見
この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: “エネルギー保存の法則” – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2015年8月)
19世紀の中ごろ、ロベルト・マイヤー、ジェームズ・プレスコット・ジュール、ヘルマン・フォン・ヘルムホルツらが、それぞれ独立して「エネルギー保存の法則」という考え方に辿りついた[1]。
マイヤーは、ドイツの医者で、船医としてジャワ島に行った時に熱量とエネルギーとの関係を考察するようになった。船が熱帯を航海すると水夫らの静脈の血液の赤みが増すことに気付き、気温が上昇したことで体温維持のために酸素が使われる量が減るのだ、と解釈した。
そして1842年、「熱」と「仕事」の関係に関する論文 „Bemerkung über die Kräfte der unbelebten Natur”[注 1]を発表した[5]。
ジュールは1843年に熱の仕事当量の測定を行い、その後も様々な方法で熱の仕事当量を計測した。
ヘルムホルツは、サディ・カルノーやエミール・クラペイロン、ジュールらの仕事について整理し、1847年に著した „Über die Erhaltung der Kraft”[注 2]で様々な状況でエネルギー保存の法則が成り立つことを示した[6]。
マイヤーやジュールが熱の仕事当量に関する考察をした頃は、1798年のベンジャミン・トンプソン(ランフォード伯)による指摘などがあったものの、アントワーヌ・ラヴォアジエとピエール=シモン・ラプラスに始まるカロリック説が有力であり、熱は物質であると見なされ、熱は単独で保存されると考えられていた。そのため、熱が仕事に変わり得ることの発見とその事実の定量的評価をすることは、熱力学第一法則を構成する上で重要な仕事だった。
1850年、ルドルフ・クラウジウスは論文 „Über die bewegende Kraft der Wärme”[注 3]の中で熱力学第一法則について完全な形で述べた[7][8]。
ジュール (1818 – 1889) は、重りをある高さまで持ち上げて落とすことで上記の装置 (今日 Joule’s Apparatus と呼ばれる)の撹拌翼を回転させ、水に摩擦熱を与えることによる温度変化を調べた。その結果、仕事と熱は等価なものであると考えられるようになり、エネルギー保存の法則の成立へと繋がった。
質量とエネルギーの等価性
1905年にアルベルト・アインシュタインは、Annus Mirabilis papers の一つの „Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?”[注 4]において、質量とエネルギーが交換可能なのではないか、という提案を行った[9][10]。これをきっかけとして、物理学が大きく変容していくことになった。「エネルギー」や「物質」という概念自体が大きく変わっていくことになったのである。
特殊相対性理論において、質量はエネルギーの一形態であり、E=mc² という式の関係が成り立っている。したがって相対論の立場では、エネルギー保存の法則は「質量を含めたエネルギーの総和が保存されている」という主張になる。
他の物理学の様々な主張同様に、このアインシュタインの主張も最初は受け入れられなかったり疑問視されたが、原子核反応や電子対生成などの実験において成立していることが確認されると、アインシュタインの考えが次第に受け入れられるようになっていった。
なおそれに伴って、「質量保存の法則は(厳密に言えば)成り立っていない」と考えられるようになった。特に、原子核反応を扱う場合においては、質量のエネルギーへの変換は無視できないほど大きく、質量は保存されていない、として計算するようになっている[注 5]。
ただし、この法則を一応受け入れるとしても、一体どの程度まで受け入れてよいのかということについて見解はバラバラであった。例えばニールス・ボーアは、ベータ崩壊をエネルギー保存の法則が成立していない事例だと考えていた[11]。
ただしそのような状況の中で、1932年にヴォルフガング・パウリとエンリコ・フェルミが、ベータ崩壊の事例でも、仮にエネルギー保存の法則が成立していると仮定して計算したところ、中性の粒子が存在しているだろう、と予想することができた。彼らはその粒子の存在を主張したものの具体的な物証は無く、長らく認められなかったが、1956年になり実験によってその粒子(ニュートリノ)が確認された。この出来事によって、有効範囲については疑問視されることも多かったものの、エネルギー保存の法則が成り立つと仮定してみることが、科学的発見につながるひとつの指針にもなり得ることが知られるようになった。
対称性
1918年、エミー・ネーターは論文 „Invariante Variationsprobleme”[注 6]を出版した[12][13]。この論文の中で、ネーターが1915年に得た、今日ネーターの定理と呼ばれる定理の証明が与えられた。ネーターの定理から、作用積分が不変であるような無限小変換が存在する場合、系はその変換に対して対称であるという。このとき系の対称性に対応した量が保存する。特にエネルギー保存の法則は、時間の並進対称性に対応していることが知られる[14]。
各分野において
熱力学
→詳細は「熱力学第一法則」を参照
熱力学におけるエネルギー保存の法則は、熱力学第一法則である。熱力学第一法則は次のように表現される。
d
U
δ
Q
−
δ
W
.
{\displaystyle dU=\delta Q-\delta W.}
ここで dU は系の内部エネルギー U の変化量、δQ は系に与えられた熱量、δW は系から取り出された仕事を表す(d は完全微分を、δ は不完全微分(英語版)を表す)。仕事は熱力学的系に繋がっている力学的系へのエネルギーの移動を表し、熱はそれ以外の熱力学的系へのエネルギーの移動を表している。
熱力学第一法則は、エネルギーがひとりでに消えたり生じたりすることはない、という経験的事実を法則化したものであり、上述の定式化では、エネルギーの変化が熱と仕事の和として与えられることで表現されている。
熱力学において第一法則は、上式を満たす状態量(すなわち系に対する操作の方法や途中経過に依存しない量[15]) U が存在することを主張する法則とみなされている[16]。
古典力学
古典力学におけるエネルギー保存の法則は、力学的エネルギー保存の法則と呼ばれる。力学的エネルギーは位置エネルギーと運動エネルギーに分類され、それらの和が一定であることをいう[17]。
一粒子系での力学的エネルギー保存の法則
以下に一粒子系の場合についての力学的エネルギー保存の法則を述べる。
一粒子の運動について、粒子に働く力
F
(
r
(
t
)
,
t
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {r}}(t),t)} がポテンシャル
V
(
r
(
t
)
)
{\displaystyle V({\boldsymbol {r}}(t))} を用いて、
F
(
r
(
t
)
,
t
)
−
∇
V
(
r
(
t
)
)
+
f
(
t
)
{\displaystyle {\boldsymbol {F}}({\boldsymbol {r}}(t),t)=-\nabla V({\boldsymbol {r}}(t))+{\boldsymbol {f}}(t)}
と表される場合について、ニュートン力学の運動の第2法則、
m
d
2
r
d
t
2
(
t
)
F
(
r
(
t
)
,
t
)
{\displaystyle m{\frac {d^{2}{\boldsymbol {r}}}{dt^{2}}}(t)={\boldsymbol {F}}({\boldsymbol {r}}(t),t)}
より次の運動方程式が得られる。
m
d
2
r
d
t
2
(
t
)
−
∇
V
(
r
(
t
)
)
+
f
(
t
)
.
{\displaystyle m{\frac {d^{2}{\boldsymbol {r}}}{dt^{2}}}(t)=-\nabla V({\boldsymbol {r}}(t))+{\boldsymbol {f}}(t).}
ここで、
m
{\displaystyle m} は質量、
r
{\displaystyle {\boldsymbol {r}}} は粒子の位置、
t
{\displaystyle t} は時刻をそれぞれ表し、ナブラ
∇
{\displaystyle \nabla } とポテンシャル
V
{\displaystyle V} の積
∇
V
{\displaystyle \nabla V} はポテンシャルの勾配を意味する。
∇
V
(
r
(
t
)
)
(
∂
∂
x
V
(
r
(
t
)
)
,
∂
∂
y
V
(
r
(
t
)
)
,
∂
∂
z
V
(
r
(
t
)
)
)
T
.
{\displaystyle \nabla V({\boldsymbol {r}}(t))=\left({\frac {\partial }{\partial x}}V({\boldsymbol {r}}(t)),{\frac {\partial }{\partial y}}V({\boldsymbol {r}}(t)),{\frac {\partial }{\partial z}}V({\boldsymbol {r}}(t))\right)^{T}.}
このとき仕事は、
W
(
t
1
,
t
2
)
∫
t
1
t
2
F
(
r
(
t
)
,
t
)
⋅
d
r
(
t
)
∫
t
1
t
2
{
−
∇
V
(
r
(
t
)
)
+
f
(
t
)
}
⋅
d
r
(
t
)
{\displaystyle {\begin{aligned}W(t_{1},t_{2})&=\int {t{1}}^{t_{2}}{\boldsymbol {F}}({\boldsymbol {r}}(t),t)\cdot d{\boldsymbol {r}}(t)\&=\int {t{1}}^{t_{2}}\left{-\nabla V({\boldsymbol {r}}(t))+{\boldsymbol {f}}(t)\right}\cdot d{\boldsymbol {r}}(t)\end{aligned}}}
と
r
(
t
)
{\displaystyle {\boldsymbol {r}}(t)} についての線積分で表される。ここで中黒 ‘・’ はベクトル空間の内積[注 7]を意味する。線積分を時間についての積分に直せば、
W
(
t
1
,
t
2
)
−
∫
t
1
t
2
∇
V
(
r
(
t
)
)
⋅
d
r
(
t
)
+
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
−
∫
t
1
t
2
{
∂
V
(
r
(
t
)
)
∂
x
d
x
(
t
)
d
t
+
∂
V
(
r
(
t
)
)
∂
y
d
y
(
t
)
d
t
+
∂
V
(
r
(
t
)
)
∂
z
d
z
(
t
)
d
t
}
d
t
+
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
,
{\displaystyle {\begin{aligned}W(t_{1},t_{2})&=-\int {t{1}}^{t_{2}}\nabla V({\boldsymbol {r}}(t))\cdot d{\boldsymbol {r}}(t)+\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t)\&=-\int {t{1}}^{t_{2}}\left{{\frac {\partial V({\boldsymbol {r}}(t))}{\partial x}}{\frac {dx(t)}{dt}}+{\frac {\partial V({\boldsymbol {r}}(t))}{\partial y}}{\frac {dy(t)}{dt}}+{\frac {\partial V({\boldsymbol {r}}(t))}{\partial z}}{\frac {dz(t)}{dt}}\right}dt+\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t),\end{aligned}}}
となるので、ポテンシャルの時間についての全微分、
d
V
d
t
(
r
(
t
)
)
{
d
x
(
t
)
d
t
∂
∂
x
+
d
y
(
t
)
d
t
∂
∂
y
+
d
z
(
t
)
d
t
∂
∂
z
}
V
(
r
(
t
)
)
{\displaystyle {\frac {dV}{dt}}({\boldsymbol {r}}(t))=\left{{\frac {dx(t)}{dt}}{\frac {\partial }{\partial x}}+{\frac {dy(t)}{dt}}{\frac {\partial }{\partial y}}+{\frac {dz(t)}{dt}}{\frac {\partial }{\partial z}}\right}V({\boldsymbol {r}}(t))}
を用いて、
W
(
t
1
,
t
2
)
−
∫
t
1
t
2
d
V
(
r
(
t
)
)
d
t
d
t
+
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
−
{
V
(
r
(
t
2
)
)
−
V
(
r
(
t
1
)
)
}
+
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
{\displaystyle {\begin{aligned}W(t_{1},t_{2})&=-\int {t{1}}^{t_{2}}{\frac {dV({\boldsymbol {r}}(t))}{dt}}dt+\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t)\&=-\left{V({\boldsymbol {r}}(t_{2}))-V({\boldsymbol {r}}(t_{1}))\right}+\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t)\end{aligned}}}
と書ける。もし、粒子が受ける力がポテンシャルのみによる場合、
f
(
t
)
{\displaystyle {\boldsymbol {f}}(t)} は存在しないので、粒子に与えられた仕事
W
(
t
1
,
t
2
)
{\displaystyle W(t_{1},t_{2})} はポテンシャルの差
−
{
V
(
r
(
t
2
)
)
−
V
(
r
(
t
1
)
)
}
{\displaystyle -\left{V({\boldsymbol {r}}(t_{2}))-V({\boldsymbol {r}}(t_{1}))\right}} に等しい。このときポテンシャル
V
(
r
(
t
)
)
{\displaystyle V({\boldsymbol {r}}(t))} は位置エネルギー[注 8]と呼ばれる。
再び仕事の定義に戻ると、粒子の運動方程式より、次のように書き換えられる。
W
(
t
1
,
t
2
)
∫
t
1
t
2
F
(
r
(
t
)
,
t
)
⋅
d
r
(
t
)
∫
t
1
t
2
m
d
2
d
t
2
r
(
t
)
⋅
d
r
(
t
)
m
∫
t
1
t
2
d
2
d
t
2
r
(
t
)
⋅
d
r
(
t
)
d
t
d
t
{\displaystyle {\begin{aligned}W(t_{1},t_{2})&=\int {t{1}}^{t_{2}}{\boldsymbol {F}}({\boldsymbol {r}}(t),t)\cdot d{\boldsymbol {r}}(t)\&=\int {t{1}}^{t_{2}}m{\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}(t)\cdot d{\boldsymbol {r}}(t)\&=m\int {t{1}}^{t_{2}}{\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}(t)\cdot {\frac {d{\boldsymbol {r}}(t)}{dt}}dt\end{aligned}}}
ここで、ベクトルの内積の微分について、
d
d
t
(
u
(
t
)
⋅
v
(
t
)
)
∑
α
x
,
y
,
z
d
d
t
(
u
α
(
t
)
v
α
(
t
)
)
∑
α
x
,
y
,
z
(
d
u
α
(
t
)
d
t
v
α
(
t
)
+
u
α
(
t
)
d
v
α
(
t
)
d
t
)
d
u
(
t
)
d
t
⋅
v
(
t
)
+
u
(
t
)
⋅
d
v
(
t
)
d
t
{\displaystyle {\begin{aligned}{\frac {d}{dt}}\left({\boldsymbol {u}}(t)\cdot {\boldsymbol {v}}(t)\right)&=\sum {\alpha =x,y,z}{\frac {d}{dt}}\left(u{\alpha }(t)v_{\alpha }(t)\right)\&=\sum {\alpha =x,y,z}\left({\frac {du{\alpha }(t)}{dt}}v_{\alpha }(t)+u_{\alpha }(t){\frac {dv_{\alpha }(t)}{dt}}\right)\&={\frac {d{\boldsymbol {u}}(t)}{dt}}\cdot {\boldsymbol {v}}(t)+{\boldsymbol {u}}(t)\cdot {\frac {d{\boldsymbol {v}}(t)}{dt}}\end{aligned}}}
という公式が成り立つので、
W
(
t
1
,
t
2
)
m
∫
t
1
t
2
d
2
d
t
2
r
(
t
)
⋅
d
r
(
t
)
d
t
d
t
m
∫
t
1
t
2
{
d
d
t
(
d
r
(
t
)
d
t
⋅
d
r
(
t
)
d
t
)
−
d
r
(
t
)
d
t
⋅
d
2
r
(
t
)
d
t
2
}
d
t
1
2
m
∫
t
1
t
2
d
d
t
(
d
r
(
t
)
d
t
⋅
d
r
(
t
)
d
t
)
d
t
1
2
m
|
d
r
(
t
2
)
d
t
|
2
−
1
2
m
|
d
r
(
t
1
)
d
t
|
2
{\displaystyle {\begin{aligned}W(t_{1},t_{2})&=m\int {t{1}}^{t_{2}}{\frac {d^{2}}{dt^{2}}}{\boldsymbol {r}}(t)\cdot {\frac {d{\boldsymbol {r}}(t)}{dt}}dt\&=m\int {t{1}}^{t_{2}}\left{{\frac {d}{dt}}\left({\frac {d{\boldsymbol {r}}(t)}{dt}}\cdot {\frac {d{\boldsymbol {r}}(t)}{dt}}\right)-{\frac {d{\boldsymbol {r}}(t)}{dt}}\cdot {\frac {d^{2}{\boldsymbol {r}}(t)}{dt^{2}}}\right}dt\&={\frac {1}{2}}m\int {t{1}}^{t_{2}}{\frac {d}{dt}}\left({\frac {d{\boldsymbol {r}}(t)}{dt}}\cdot {\frac {d{\boldsymbol {r}}(t)}{dt}}\right)dt\&={\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{2})}{dt}}\right|^{2}-{\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{1})}{dt}}\right|^{2}\end{aligned}}}
が得られる。ここで得られた関数
1
2
m
|
d
r
(
t
)
d
t
|
2
{\displaystyle {\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t)}{dt}}\right|^{2}} は粒子の運動エネルギーと呼ばれ、この差分は粒子になされた仕事を表す。
ポテンシャルと仕事、運動エネルギーと仕事の関係をそれぞれ見比べると、
−
{
V
(
r
(
t
2
)
)
−
V
(
r
(
t
1
)
)
}
+
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
1
2
m
|
d
r
(
t
2
)
d
t
|
2
−
1
2
m
|
d
r
(
t
1
)
d
t
|
2
∫
t
1
t
2
f
(
t
)
⋅
d
r
(
t
)
{
1
2
m
|
d
r
(
t
2
)
d
t
|
2
+
V
(
r
(
t
2
)
)
}
−
{
1
2
m
|
d
r
(
t
1
)
d
t
|
2
+
V
(
r
(
t
1
)
)
}
{\displaystyle {\begin{aligned}-\left{V({\boldsymbol {r}}(t_{2}))-V({\boldsymbol {r}}(t_{1}))\right}+\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t)&={\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{2})}{dt}}\right|^{2}-{\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{1})}{dt}}\right|^{2}\\int {t{1}}^{t_{2}}{\boldsymbol {f}}(t)\cdot d{\boldsymbol {r}}(t)&=\left{{\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{2})}{dt}}\right|^{2}+V({\boldsymbol {r}}(t_{2}))\right}-\left{{\frac {1}{2}}m\left|{\frac {d{\boldsymbol {r}}(t_{1})}{dt}}\right|^{2}+V({\boldsymbol {r}}(t_{1}))\right}\end{aligned}}}
という等式が得られる。
f
(
t
)
{\displaystyle {\boldsymbol {f}}(t)} を粒子に対する力学的な操作によって生じる力だとすれば、それがなす仕事は操作の前後での粒子の力学的エネルギー、すなわち粒子の位置エネルギーと運動エネルギーの和、の差に等しい。特に、外部から力学的操作を行わない場合には、粒子にはポテンシャルによる力しか働かないので、系の力学的エネルギーは保存されることになる。また、操作の前後で粒子の速度を変えないようにすれば[注 9]、操作の前後では粒子の運動エネルギーが変化しないので、外部から与えられた仕事は粒子のポテンシャルの差に等しくなる。
こうして得られた等式が成り立つことを、力学的エネルギー保存の法則と呼ぶ。保存則が成り立っているかどうかは系の設定により、外界の力学的エネルギーを考慮しない場合には、保存則は成り立たないが、外界の力学的エネルギーを考慮するのであれば、外界への仕事を付け加える形で、保存則が成立する。
外界に及ぼされる力は
−
f
(
t
)
{\displaystyle -{\boldsymbol {f}}(t)} で表され、摩擦などによる抗力を考える場合には、粒子の速度の関数になる。
多粒子系での力学的エネルギー保存の法則
以上のことは多粒子系の場合にも成り立つ。一粒子系の場合との変更点は、各粒子に対して力と運動方程式が与えられることと、ポテンシャルがすべての粒子の位置の関数になることである。以下にN 個の粒子がある場合について示す。
力:
F
i
(
{
r
(
t
)
}
,
t
)
−
∇
i
V
(
{
r
i
(
t
)
}
)
+
f
i
(
t
)
(
i
1
,
…
,
N
)
.
{\displaystyle {\boldsymbol {F}}{i}({{\boldsymbol {r}}(t)},t)=-\nabla {i}V({{\boldsymbol {r}}{i}(t)})+{\boldsymbol {f}}{i}(t)\quad (i=1,\dots ,N).}
運動方程式:
m
i
d
2
r
i
d
t
2
(
t
)
F
i
(
{
r
(
t
)
}
,
t
)
(
i
1
,
…
,
N
)
.
{\displaystyle m_{i}{\frac {d^{2}{\boldsymbol {r}}{i}}{dt^{2}}}(t)={\boldsymbol {F}}{i}({{\boldsymbol {r}}(t)},t)\quad (i=1,\dots ,N).}
ナブラ
∇
i
{\displaystyle \nabla _{i}} は、粒子
i
{\displaystyle i} の位置に対する偏微分を表し、ポテンシャルの勾配は次のように変更される。
∇
i
V
(
{
r
i
(
t
)
}
)
(
∂
∂
x
i
V
(
{
r
i
(
t
)
}
)
,
∂
∂
y
i
V
(
{
r
i
(
t
)
}
)
,
∂
∂
z
i
V
(
{
r
i
(
t
)
}
)
)
T
(
i
1
,
…
,
N
)
.
{\displaystyle \nabla {i}V({{\boldsymbol {r}}{i}(t)})=\left({\frac {\partial }{\partial x_{i}}}V({{\boldsymbol {r}}{i}(t)}),{\frac {\partial }{\partial y{i}}}V({{\boldsymbol {r}}{i}(t)}),{\frac {\partial }{\partial z{i}}}V({{\boldsymbol {r}}_{i}(t)})\right)^{T}\quad (i=1,\dots ,N).}
また、ポテンシャルの時間微分は、それぞれの粒子の速度と粒子が感じるポテンシャルの勾配の内積をすべて足しあわせたものになる。
d
V
d
t
(
{
r
i
(
t
)
}
)
∑
i
1
N
d
r
i
(
t
)
d
t
⋅
∇
i
V
(
{
r
i
(
t
)
}
)
.
{\displaystyle {\frac {dV}{dt}}({{\boldsymbol {r}}{i}(t)})=\sum {i=1}^{N}{\frac {d{\boldsymbol {r}}{i}(t)}{dt}}\cdot \nabla {i}V({{\boldsymbol {r}}_{i}(t)}).}
系になされる仕事は、各粒子に対する仕事の和になる。
W
(
t
1
,
t
2
)
∑
i
1
N
∫
t
1
t
2
F
i
(
{
r
i
(
t
)
}
,
t
)
⋅
d
r
i
(
t
)
.
{\displaystyle W(t_{1},t_{2})=\sum {i=1}^{N}\int {t_{1}}^{t_{2}}{\boldsymbol {F}}{i}({{\boldsymbol {r}}{i}(t)},t)\cdot d{\boldsymbol {r}}_{i}(t).}
以上のことから、力学的エネルギー保存の法則は次のように表される。
∑
i
1
N
∫
t
1
t
2
f
i
(
t
)
⋅
d
r
i
(
t
)
{
V
(
{
r
i
(
t
2
)
}
)
+
∑
i
1
N
(
1
2
m
i
|
d
r
i
(
t
2
)
d
t
|
2
)
}
−
{
V
(
{
r
i
(
t
1
)
}
)
+
∑
i
1
N
(
1
2
m
i
|
d
r
i
(
t
1
)
d
t
|
2
)
}
.
{\displaystyle \sum {i=1}^{N}\int {t_{1}}^{t_{2}}{\boldsymbol {f}}{i}(t)\cdot d{\boldsymbol {r}}{i}(t)=\left{V({{\boldsymbol {r}}{i}(t{2})})+\sum {i=1}^{N}\left({\frac {1}{2}}m{i}\left|{\frac {d{\boldsymbol {r}}{i}(t{2})}{dt}}\right|^{2}\right)\right}-\left{V({{\boldsymbol {r}}{i}(t{1})})+\sum {i=1}^{N}\left({\frac {1}{2}}m{i}\left|{\frac {d{\boldsymbol {r}}{i}(t{1})}{dt}}\right|^{2}\right)\right}.}
一粒子の場合と異なり、各粒子の運動エネルギーの総和と系のポテンシャルの和が系の力学的エネルギーの役割を果たしている[注 10]。
量子力学
量子力学においてもエネルギー保存の法則は厳密に成立する。量子力学において、あらゆる物理量はそれに対応するエミルート作用素として定義される[注 11]。閉じた系のエネルギーを与える作用素は、古典力学のハミルトニアンに対応する作用素
H
^
{\displaystyle {\hat {H}}} である[注 12]。
物理量
O
^
{\displaystyle {\hat {O}}} の期待値の時間微分を計算すると、
d
d
t
⟨
ψ
|
O
^
|
ψ
⟩
(
∂
∂
t
|
ψ
⟩
∗
)
O
^
|
ψ
⟩
+
|
ψ
⟩
∗
∂
∂
t
O
^
|
ψ
⟩
i
ℏ
(
−
ℏ
i
∂
∂
t
|
ψ
⟩
)
∗
O
^
|
ψ
⟩
+
|
ψ
⟩
∗
i
ℏ
ℏ
i
∂
∂
t
O
^
|
ψ
⟩
i
ℏ
{
(
H
^
|
ψ
⟩
)
∗
O
^
|
ψ
⟩
+
|
ψ
⟩
∗
ℏ
i
(
∂
O
^
∂
t
+
O
^
∂
∂
t
)
|
ψ
⟩
}
i
ℏ
{
|
ψ
⟩
∗
H
^
∗
O
^
|
ψ
⟩
+
|
ψ
⟩
∗
(
ℏ
i
∂
O
^
∂
t
−
O
^
H
^
)
|
ψ
⟩
}
⟨
ψ
|
(
∂
O
^
∂
t
+
i
ℏ
{
H
^
O
^
−
O
^
H
^
}
)
|
ψ
⟩
{\displaystyle {\begin{aligned}{\frac {d}{dt}}\left\langle \psi \right\vert {\hat {O}}\left\vert \psi \right\rangle &=\left({\frac {\partial }{\partial t}}\left\vert \psi \right\rangle ^{}\right){\hat {O}}\left\vert \psi \right\rangle +\left\vert \psi \right\rangle ^{}{\frac {\partial }{\partial t}}{\hat {O}}\left\vert \psi \right\rangle \&={\frac {i}{\hbar }}\left(-{\frac {\hbar }{i}}{\frac {\partial }{\partial t}}\left\vert \psi \right\rangle \right)^{}{\hat {O}}\left\vert \psi \right\rangle +\left\vert \psi \right\rangle ^{}{\frac {i}{\hbar }}{\frac {\hbar }{i}}{\frac {\partial }{\partial t}}{\hat {O}}\left\vert \psi \right\rangle \&={\frac {i}{\hbar }}\left{\left({\hat {H}}\left\vert \psi \right\rangle \right)^{}{\hat {O}}\left\vert \psi \right\rangle +\left\vert \psi \right\rangle ^{}{\frac {\hbar }{i}}\left({\frac {\partial {\hat {O}}}{\partial t}}+{\hat {O}}{\frac {\partial }{\partial t}}\right)\left\vert \psi \right\rangle \right}\&={\frac {i}{\hbar }}\left{\left\vert \psi \right\rangle ^{}{\hat {H}}^{}{\hat {O}}\left\vert \psi \right\rangle +\left\vert \psi \right\rangle ^{*}\left({\frac {\hbar }{i}}{\frac {\partial {\hat {O}}}{\partial t}}-{\hat {O}}{\hat {H}}\right)\left\vert \psi \right\rangle \right}\&=\left\langle \psi \right\vert \left({\frac {\partial {\hat {O}}}{\partial t}}+{\frac {i}{\hbar }}\left{{\hat {H}}{\hat {O}}-{\hat {O}}{\hat {H}}\right}\right)\left\vert \psi \right\rangle \end{aligned}}}
となり、
O
^
{\displaystyle {\hat {O}}} の時間発展を記述する作用素が得られる。ここでシュレーディンガー方程式、
H
^
|
ψ
(
t
)
⟩
−
ℏ
i
∂
∂
t
|
ψ
(
t
)
⟩
{\displaystyle {\hat {H}}\left\vert \psi (t)\right\rangle =-{\frac {\hbar }{i}}{\frac {\partial }{\partial t}}\left\vert \psi (t)\right\rangle }
を用い時間微分作用素をハミルトニアンに書き換えた。またハミルトニアンが自己共役であることを用いた。
O
^
{\displaystyle {\hat {O}}} がハミルトニアンであるなら、交換子の項はゼロになる。
[
H
^
,
O
^
]
:=
H
^
O
^
−
O
^
H
^
H
^
H
^
−
H
^
H
^
0.
{\displaystyle \left[{\hat {H}},{\hat {O}}\right]:={\hat {H}}{\hat {O}}-{\hat {O}}{\hat {H}}={\hat {H}}{\hat {H}}-{\hat {H}}{\hat {H}}=0.}
このとき期待値の時間微分は以下のようになる。
d
d
t
⟨
ψ
|
H
^
|
ψ
⟩
⟨
ψ
|
∂
H
^
∂
t
|
ψ
⟩
.
{\displaystyle {\frac {d}{dt}}\left\langle \psi \right\vert {\hat {H}}\left\vert \psi \right\rangle =\left\langle \psi \right\vert {\frac {\partial {\hat {H}}}{\partial t}}\left\vert \psi \right\rangle .}
外部系との相互作用がない孤立系を考えると、ハミルトニアン
H
^
{\displaystyle {\hat {H}}} にはあらわな時間依存性がないので、エネルギー保存の法則が成り立っている。
∂
H
^
∂
t
0
⇒
d
d
t
⟨
ψ
|
H
^
|
ψ
⟩
0.
{\displaystyle {\frac {\partial {\hat {H}}}{\partial t}}=0~\Rightarrow ~{\frac {d}{dt}}\left\langle \psi \right\vert {\hat {H}}\left\vert \psi \right\rangle =0.}
時間とエネルギーの不確定性関係のために短時間ではエネルギー保存則が破れるという記述もあるが、それは摂動論における自由ハミルトニアン部分の保存則の破れにすぎず、相互作用項まで加えた全エネルギーは常に厳密に保存する(詳しくは不確定性原理のページを参照)。
注意
この節は検証可能な参考文献や出典が全く示されていないか、不十分です。 出典を追加して記事の信頼性向上にご協力ください。(このテンプレートの使い方)
出典検索?: “エネルギー保存の法則” – ニュース · 書籍 · スカラー · CiNii · J-STAGE · NDL · dlib.jp · ジャパンサーチ · TWL (2012年11月)
「《エネルギー保存の法則》が成り立つ」ということは「(有用な)エネルギーはいくら使ってもなくならない」という意味ではない(第二種永久機関の否定)。エネルギー保存の法則は、エネルギー問題においては直接的には第一種永久機関の否定という面でかかわりを持つ。
脚注
[脚注の使い方]
注釈
^ Remark upon the Forces of the Inanimate Nature, 無生物界の力についての所見。
^ On the Conservation of the Force.
^ On the Moving Force of the Heat.
^ このドイツ語を英語に翻訳すると、”Does the inertia of a body depend upon its energy-content? ” となる。
^ 厳密には成立していないが、ごく平凡な古典力学的な状況設定や、ごく平凡な化学反応においては、質量の増減は無視できるほど小さく、成立しているとして扱っても問題ないので、現在でも“質量保存則”は様々な計算をするための簡便な近似として用いられている。
^ Invariant Variation Problems.
^ 一般の内積と区別して、しばしばドット積(点乗積)と呼ばれる。
^ ポテンシャル・エネルギーとも書かれる。
^ 方程式から明らかなように、操作の途中においては粒子の運動エネルギーを変化させてよい。
^ ポテンシャル
V
(
{
r
i
(
t
)
}
)
{\displaystyle \scriptstyle V({{\boldsymbol {r}}_{i}(t)})} は一つの多粒子系に対して与えられることに注意。
^ 物理学の文献では自己共役作用素はエルミート演算子、作用素の自己共役性は演算子のエルミート性 と呼ばれることも多い。物理量の測定値が実数であること(固有値が実数であること)、その固有状態が完全系をなすなどの理由から、物理量に対応する作用素には自己共役性が課される。
^ こちらの作用素もハミルトニアンと呼ぶ。区別する場合には、「古典力学のハミルトニアン」、「量子力学のハミルトニアン」と呼ぶが、単にハミルトニアンという場合には量子力学における作用素を指すことが多い。
出典
^ a b 朝永振一郎『物理学読本』(第2)みすず書房、1981年、78頁。ISBN 4-622-02503-5。
^ ウィキソース出典 Renatus Cartesius (ラテン語), Principia philosophiae, ウィキソースより閲覧。
^ a b Daniel Garber (1992). “Descartes’ Physics”. In John Cottingham. The Cambridge Companion to Descartes. Cambridge University Press. pp. 310–319. ISBN 0-521-36696-8
^ William John Macquorn Rankine C.E.F.R.S.E.F.R.S.S.A. (1853), “On the general Law of the Transformation of Energy”, Philosophical Magazine, 4 5 (30): 106-117, doi:10.1080/14786445308647205
^ J. R. Mayer (1842), Justus Liebig (Editor), “Bemerkung über die Kräfte der unbelebten Natur”, Annalen der Chemie und Pharmacie 42: 233-240.
^ Hermann von Helmholtz (1847), Über die Erhaltung der Kraft, G. Reimer Berlin.
^ R. Clausius (1850), “Über die bewegende Kraft der Wärme , Part I, Part II”, Annalen der Physik 79: 368–397, 500–524.
^ R. Clausius (1851), “On the Moving Force of Heat, and the Laws regarding the Nature of Heat itself which are deducible therefrom”, Phil. Mag., 4 2: 1–21, 102–119. Google Books. Clausius 1850 の英訳版。
^ A. Einstein, Ist die Trägheit eines Körpers von seinem Energieinhalt abhängig?, Annalen der Physik 18: pp.639–641, 1905.
^ A. Einstein, Does the Inertia of a Body depend upon its Energy-Content?, 1905. John Walker (fourmilab.ch) による英訳版 (pdf)。
^ 武谷 三男, 豊田 利幸, 中村 誠太郎『現代物理学(原子核)』 第八巻、岩波書店〈岩波講座〉、1959年、197–201頁。
^ E. Nöther (1918), “Invariante Variationsprobleme”, Nachrichten von der königliche Geselschaft der Wissenschaften zu Göttingen: 235-257.
^ E. Noether (1918), Invariant Variation Problems. M. A. Tavel による英訳。
^ 須藤靖『解析力学・量子論』(初)東京大学出版会、2008年、39-41頁。ISBN 978-4-13-062610-1。
^ 田崎晴明『熱力学 現代的な視点から』培風館、2000年、59頁。ISBN 4-563-02432-5。
^ 久保亮五 編『大学演習 熱学・統計力学』(修訂)裳華房、1998年、5頁。ISBN 4-7853-8032-2。
^ 朝永振一郎『物理学読本』(第2)みすず書房、1981年、74頁。ISBN 4-622-02503-5。
関連項目
物理学の法則
熱力学第零法則
熱力学第二法則
熱力学第三法則
質量保存の法則
ヘスの法則
物理学に関係する人物
ベンジャミン・トンプソン(ラムフォード伯)
ニコラ・レオナール・サディ・カルノー
エミール・クラペイロン
ユリウス・ロベルト・フォン・マイヤー
ジェームズ・プレスコット・ジュール
ヘルマン・フォン・ヘルムホルツ
ウィリアム・トムソン(ケルビン卿)
外部リンク
『エネルギー保存の法則』 – コトバンク
典拠管理データベース ウィキデータを編集
国立図書館
ドイツアメリカフランスBnF dataチェコラトビアイスラエル
その他
Yale LUX
カテゴリ: エネルギー熱力学の法則保存則量子力学
最終更新 2025年9月11日 (木) 09:28 (日時は個人設定で未設定ならばUTC)。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。』