逆数
https://ja.wikipedia.org/wiki/%E9%80%86%E6%95%B0

『出典: フリー百科事典『ウィキペディア（Wikipedia）』

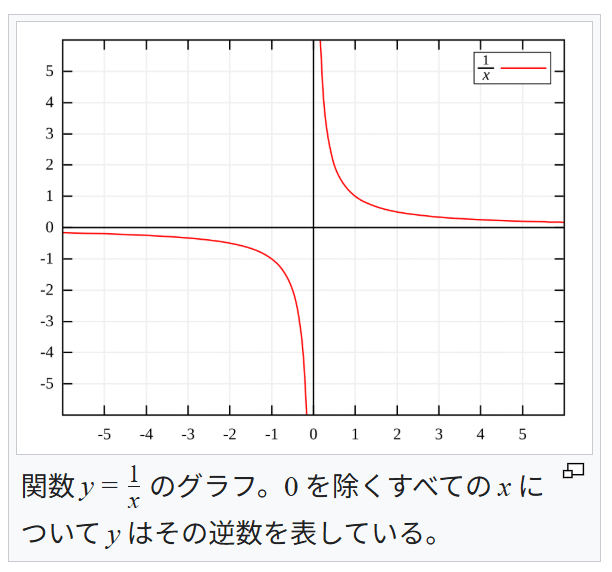
関数 y =
1
/
x
のグラフ。0 を除くすべての x について y はその逆数を表している。
逆数（ぎゃくすう、英: reciprocal）とは、ある数に掛け算した結果が 1 となる数である。すなわち、数 x の逆数 y とは次のような関係を満たす。

x
×

y

y
×

x

1.
{\displaystyle x\times y=y\times x=1.}
通常、x の逆数は分数の記法を用いて
1
/
x
のように表されるか、冪の記法を用いて x−1 のように表される。

1 を乗法に関する単位元と見れば、逆数とは乗法逆元（じょうほうぎゃくげん、英: multiplicative inverse）の一種であり、乗法逆元とは一般化された逆数である。

上述の式から明らかなように、x と y の役割を入れ替えれば、x は y の逆数であると言える。従って、x の逆数が y であるとき y の逆数は x である。

x が 0 である場合、任意の数との積は 0 になるため、（0 ≠ 1 であれば）0 に対する逆数は存在しない。

また、任意の x について必ずしもその逆数が存在するとは限らない。たとえば、自然数の範囲では上述の関係を満たす数は x = y = 1 以外には存在しない。0 を除く任意の数 x について逆数が常に存在するようなものには、有理数や実数、複素数がある。これらのように四則演算が自由にできる集合を体と呼ぶ。

逆数は乗法における逆元であるが、加法における逆元として反数がある。

1つの二項演算を持つ集合であって左右の逆元が常に存在するもの（代数的構造）はループと呼ばれる。

例
以下に具体例をいくつか挙げる。ここで e はネイピア数、i は虚数単位、r は複素数の絶対値、θ は複素数の偏角を表す。また、z は複素数 z の共役複素数、|a| は数 a の絶対値を表す。

9 の逆数は
1
/
9
。同様に
1
/
9
の逆数は 9。
2
/
3
の逆数は
3
/
2
。同様に
3
/
2
の逆数は
2
/
3
。
0.3 の逆数は
1
/
0.3
=
10
/
3
。同様に
10
/
3
の逆数は
3
/
10
= 0.3。
−5 の逆数は
1
/
−5
= −
1
/
5
= −0.2。
−|a| の逆数は
1
/
−|a|
= −
1
/
|a|
。
i の逆数は
1
/
i
= i−1 = −i。
3 + 4i の逆数は
1
/
3 + 4i
=
3 − 4i
/
25
。
x + yi の逆数は
1
/
x + yi
=
x − yi
/
x 2 + y 2
。
reiθ の逆数は (reiθ)−1 =
1
/
r
e−iθ。
複素数 z の逆数は
1
/
z
=
1
/
|z|2
z。
合同式での逆数
→詳細は「モジュラ逆数」を参照
合同式において逆数を考えることができる。a × b を m で割ると 1 余るとき、b を a の m を法とする逆数と呼ぶ。合同式で表すと以下のようになる。

a
×
b
≡
1
(
mod
m
)
.
{\displaystyle a\times b\equiv 1{\pmod {m}}.}
例えば、4 × 2 ≡ 1 (mod 7) となるので、法 7 において 2 は 4 の逆数である。通常の逆数と同様、逆数の逆数は同じ数であり、0 の逆数は存在せず、1 や −1 の逆数はそれ自身である。合同式の性質から、m の倍数の逆数は存在せず、(km ± 1) の逆数はそれ自身になる。

定義上、a は m と互いに素である必要がある。つまり、一般に合同式での逆数は存在するとは限らない。例えば、7 × b ≡ 1 (mod 42) や 12 × b ≡ 1 (mod 4) を満たす b は存在しない。

素数 p を法とする場合、0 以外の全ての元が逆数を持つ。法 17 を例とすると次のようになる。

元 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
逆数 なし 1 9 6 13 7 3 5 15 2 12 14 10 4 11 8 16
合同式での逆数はオイラーの定理によって計算できる。a に逆数 b が存在するならば

a
×
b
≡
1
≡
a
φ
(
m

)

a
×
a
φ
(
m
)
−
1
(
mod
m
)
{\displaystyle a\times b\equiv 1\equiv a^{\varphi (m)}=a\times a^{\varphi (m)-1}{\pmod {m}}}
なので、

b
≡
a
φ
(
m
)
−
1
(
mod
m
)
{\displaystyle b\equiv a^{\varphi (m)-1}{\pmod {m}}}
（ここで φ はオイラーのφ関数）であり、逆に a と m が互いに素であれば、この式によって逆数が与えられる。特に、m が素数の場合以下のようになる（フェルマーの小定理から直接導かれる）。

b
≡
a
m
−
2
(
mod
m
)
.
{\displaystyle b\equiv a^{m-2}{\pmod {m}}.}
また、ユークリッドの互除法によっても効率的に求めることができる。定義式は、以下のベズーの等式（ディオファントス方程式の一種）が b と n について整数解を持つことと同値である。

a
×
b
+
m
×

n

1.
{\displaystyle a\times b+m\times n=1.}
この式の解は、a と m が互いに素である場合、かつその場合に限り存在する。

日本における学校教育
日本の小学校では、小学6年生で分数の掛け算・割り算について学習する際に、逆数について学習し、x（実際には具体的な数を用いる）で割ることと
1
/
x
を掛けることが同じ結果を得ることなどを学ぶ。この事は中学校の課程で、加法における逆元、つまり負の数について学ぶ準備になっている。

関連項目
反比例
単位分数
エジプト式分数
反数
逆元
単位元
吸収元
逆行列
群 (数学)
準群#ループ
カテゴリ: 算術代数学初等数学数学に関する記事
最終更新 2024年1月14日 (日) 11:25 （日時は個人設定で未設定ならばUTC）。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。』