体 (数学)
https://ja.wikipedia.org/wiki/%E4%BD%93_(%E6%95%B0%E5%AD%A6)

『出典: フリー百科事典『ウィキペディア（Wikipedia）』

→詳細は「可換体」および「斜体 (数学)」を参照

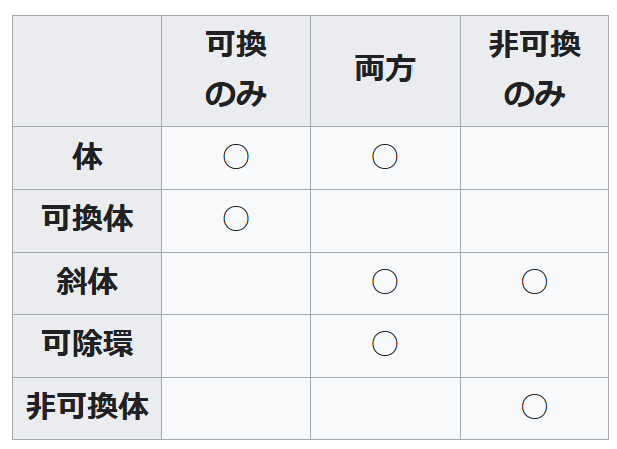
可換

のみ 両方 非可換
のみ
体 ○ ○
可換体 ○
斜体 ○ ○
可除環 ○
非可換体 ○

数学において、体（たい）とは、四則演算が（零で割ることを除いて）自由に行える代数系のことである。

体の定義においては、積が可換か非可換かに必ずしも注視しないが、積が可換かそうでないかで目的意識や手法は大きく異なる。

前者については可換体の項を、後者については斜体の項を参照されたい。

定義をきちんと述べれば、

「体とは、単位的環であって、その非零元の全体が乗法に関して群を成すものを言う」

あるいは

「体とは、非自明な単位的環であって、任意の非零元が乗法逆元を持つものを言う」

となる。

この代数的構造はリヒャルト・デーデキントとレオポルト・クロネッカーにより独立に（また極めて異なる方法で）導入されたが、ドイツ語で体を意味する Körper は、実数または複素数からなる集合で四則演算に関して閉じているものを当初は指していた。

体をしばしば文字 K で表すのはこのドイツ語名による。

体という言葉は「ある種の完全性、充足性、自己完結性を備えたシステム、つまりは自然に統合されている有機的な全体」を表すものとして選ばれた[1]。

脚注
[脚注の使い方]

^ Richard Dedekind, Theory of algebraic integers, p. 5, – Google ブックス
スタブアイコン
この項目は、抽象代数学に関連した書きかけの項目です。この項目を加筆・訂正などしてくださる協力者を求めています（プロジェクト:数学／Portal:数学）。

曖昧さ回避のアイコン

このページは数学の曖昧さ回避のためのページです。一つの語句が複数の意味・職能を有する場合の水先案内のために、異なる用法を一覧にしてあります。お探しの用語に一番近い記事を選んで下さい。このページへリンクしているページを見つけたら、リンクを適切な項目に張り替えて下さい。

カテゴリ: 曖昧さ回避数学の曖昧さ回避数学に関する記事

最終更新 2023年5月14日 (日) 07:48 （日時は個人設定で未設定ならばUTC）。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。』