行列の計算とは何を行っているのでしょうか？計算の意味というか、なにを計算させられているのか全くわかりません。なんとなくベクトルの成分計算に似ている気がするのですがベクトルは関係ありますか？
https://jp.quora.com/%E8%A1%8C%E5%88%97%E3%81%AE%E8%A8%88%E7%AE%97%E3%81%A8%E3%81%AF%E4%BD%95%E3%82%92%E8%A1%8C%E3%81%A3%E3%81%A6%E3%81%84%E3%82%8B%E3%81%AE%E3%81%A7%E3%81%97%E3%82%87%E3%81%86%E3%81%8B-%E8%A8%88%E7%AE%97%E3%81%AE

　※　今日は、「数理データサイエンスＡＩ　応用基礎講座　データサイエンス基礎　数学基礎３　ベクトルと行列」というものを、視聴した。

　※　実は、視たのは、３回目だ…。まあ、こま切れに視てるんだが…。

　※　それでも、イマイチ、よく分からんので、ちょっと調べた…。

　※　大体、この「ベクトル」というものは、オレにとっては「高校数学、最大の躓きの石」なんだよな…（他にも、あるが）。

　※　それまで、さんざん、「ベクトルというものは、他の数とはちょっと違う。単なる、「スカラー」ではないものなんだ。」という話しで進んで来た…。

　※　それなのに、いきなり「内積というものがある。これは、「スカラー」である。」とか吐かすんだよな…。

　※　そういう話しの展開に、ついて行けず、決定的に「数学コンプレックス」を抱いた…。

　※　そういう「数学コンプレックス」から、脱却し、解放されたのは、ようやく４０近くなってからだ…。

『西野 眞王
金沢大学で数学の学士号を取得 (卒業年:2021)執筆者は651件の回答を行い、558.4万回閲覧されています更新日時:3年前

そもそも行列は何を表すかというと、いろいろな解釈がありますが、もっとも重要な解釈の一つとしては、行列は「ベクトルを変化させるもの」を表します。行列をベクトルにかけると別の(あるいは同じ)ベクトルに変化しますね。

変化のさせ方には様々なしかたがあり、図形的な意味があるものとしては対称移動、スケール変換（大きさを変える)・回転などといった変化を行列は表すことができます。(2×2
の場合を考えるなら)たった4つの数字の羅列で、非常にたくさんの操作を表すことができるので、行列は非常に有用です。

つまるところ、行列というのは関数の仲間ととらえることができます。関数とは、なにか数を入れると、一定の規則にしたがって、別の、あるいは同じ数を出します。行列は、なにかベクトルをかけると、一定の規則に従って、別の、あるいは同じベクトルを出すわけです。

ただ、ベクトルに対してベクトルを返す関数はなんでも行列で表せるわけではありません。とくに、線形写像とよばれるたぐいの関数を行列は表します。

さて、「行列はベクトルを変化させる操作を表す」ということを念頭において、とくに「行列の積」という操作について見てみましょう。

行列の積は、「かけられた行列が表す操作を、合成した操作」を表します。

たとえば、平面上の話を考えましょう。A
という行列が、ベクトルを45∘の反時計まわり回転させる操作を表すとして、Bが30∘の時計回りの回転を表すとしましょう。つまりベクトルxに対しAxはxを45∘

回転させたものを表したりするわけです。

このとき、AB
という行列は、30∘の時計回りの回転をした後、45∘の反時計まわり回転をするような操作を表します。つまり、15∘

の反時計回りの回転ですね。

この言い方からわかる方もいるかもしれませんが、右にある行列があらわす操作から行われます。ふつうはベクトルを右からかけるからですね。なので、BA
という行列は45∘の回転をしてから30∘

の回転をする操作をあらわすわけです。

ただ、この場合BA
とABは同じ操作を表し、そして行列としてもAB=BAが成立してしまうので、これはちょっと悪い例です。ちょっとジョークじみた例ですが、たとえばパンツをはいてからズボンをはくのと、ズボンをはいてからパンツをはくのとでは結果は異なりますね。このように、一般にAB≠BAであり、ABとBA

が表す操作は異なります。行列の積が交換できないことはどこかで聞いたことがあるとは思いますが、それはこのように行列が「ベクトルの操作」を表し、積が「操作の合成を表す」からです。

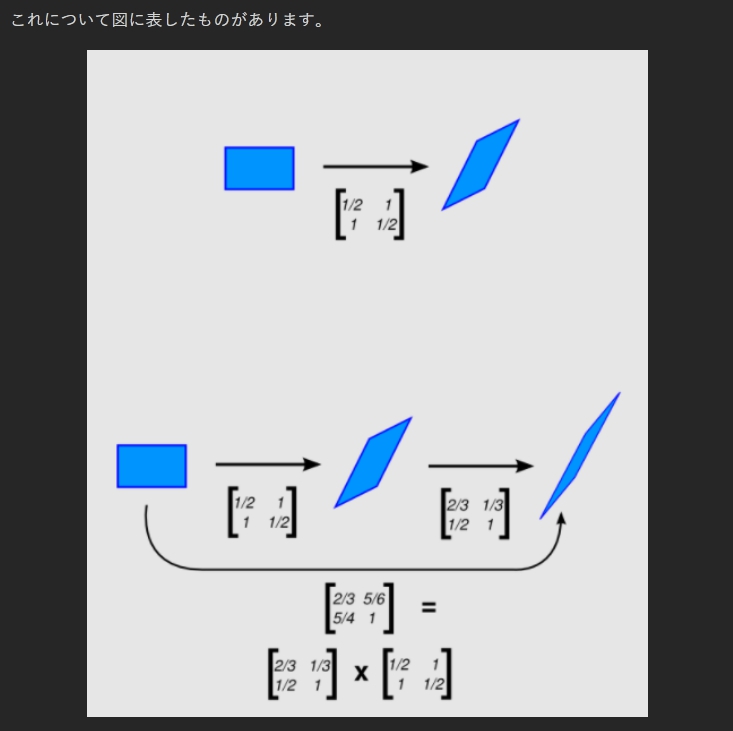
これについて図に表したものがあります。

(図はSomeone anonymous’s answer to What is the intuition behind multiplication of matrices? より抜粋。もともとこの回答を翻訳しようかと思いましたが、この回答は積だけなので…)

このように、行列はベクトルの変換や、それを通じて図形の変換を表し、そして行列の掛け算は２つの操作の合成を表します。

このように行列の積については面白いことがいえるのですが、足し算や引き算についてはあまり面白いことはいえません。上の話を踏まえていうならば、A+B
という行列は、「Aの表す操作とB

の表す操作をそれぞれ独立に行った後に、その結果を足す」という操作を表しますが、個人的にはトートロジーじみていてあまり面白くない気がします。

このように、ベクトルと行列とは海ほど深いかかわりがあります。行列はベクトルを操作するので、行列の計算もまたベクトルに近くならざるを得なかった、といえるでしょう。
閲覧数:9,082回高評価を見る
5件のシェアを表示』