行列の掛け算について、その「意味」を教えてください。
https://detail.chiebukuro.yahoo.co.jp/qa/question_detail/q11256265466

ID非公開さん

2022/1/30 12:18

6回答

『Q、行列の掛け算について、その「意味」を教えてください。

まず、（1行2列）×（2行1列）の掛け算で、縦横が異なりますが、それぞれの行・列・要素の意味がわかりません。また、なぜ横×縦に掛け合わせるのか、その意味や理由がわかりません。それぞれが何を意味しているのかを教えてください。

いろいろ本を読んでみましたが、「そういうルールだから」とか「そういう形で変形すると結果的にあってる」というような、実際の所何も説明していないような解説しかありませんでした。

（『数学ガール』の行列編も読みましたが、結局、操作方法だけのレクチャーで、なぜそうなっているのか、それぞれの要素が何を意味しているのか、まったくわかりませんでした）

掛け算の仕方や、「式を変形したらそうなる」という説明は不要です。ルールにのっとって盲目的に機械的計算をして結果を出すことはできています。

意味・理由をわかりやすく解説してください。
補足

2行2列以上の場合も含めて、わかるように教えてください。』

『fvtさん

2022/2/6 12:58
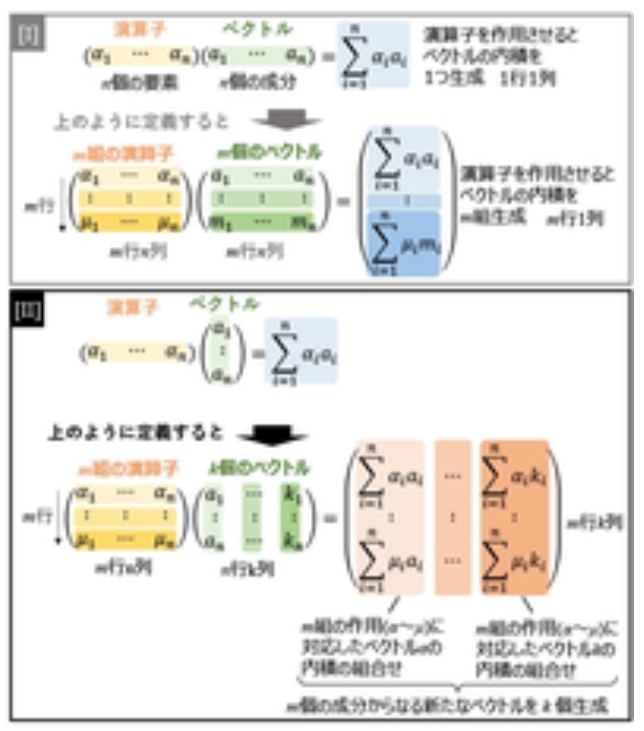
下に図を貼り付けましたが、行列の掛け算を演算子とベクトルの関係で考えると理解しやすいかもしれません。

[I] 演算子もベクトルも両方とも行で表して掛け算すると定義した場合、m個の組合せに発展させても、得られる結果は演算子とベクトルの積（内積）がそれぞれ独立にm個生成されるだけです。

{II] 演算子を行、ベクトルを列で表して掛け算すると定義した場合、m組の演算子とk個のベクトルに発展させると、各ベクトルにm組の演算子を作用させたm個の内積の組合せが生成し、それを一つのベクトルとしてみなすと、m個の成分からなるk個のベクトルが新たに生成することになります。

直感的に[II]で定義する方が発展性があると感じられるでしょう。

実際、立体や流体の応力場、電磁場を考える場合、各位置の特性を表す3次元のベクトルに、様々な影響（たとえば外部の応力場や電磁場、隣接場との相互作用など）を作用させる必要があるため、それを行列形式の演算子とし、列方式で表した各位置の特性ベクトルに掛ける[II]の定義が威力を発揮します。』