回帰分析
https://ja.wikipedia.org/wiki/%E5%9B%9E%E5%B8%B0%E5%88%86%E6%9E%90
※ 今日は、録画しといた放送大学の「数理・データサイエンス・AI専門講座(たぶん、第1回)」というものを視聴した。途中からの録画だったが…。
※ そこで出てきた、気になる「テクニカルターム」を、調べたんで貼っておく…。

『出典: フリー百科事典『ウィキペディア(Wikipedia)』
出典は列挙するだけでなく、脚注などを用いてどの記述の情報源であるかを明記してください。記事の信頼性向上にご協力をお願いいたします。(2020年2月)
曖昧さ回避 この項目では、統計学における回帰について説明しています。その他の用法については「回帰」をご覧ください。
統計学
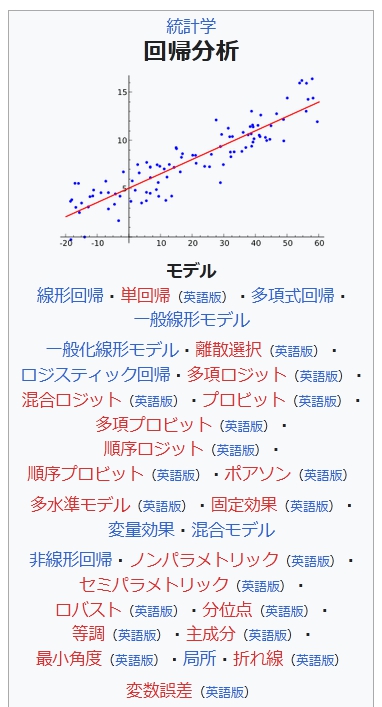
回帰分析
モデル
線形回帰 単回帰(英語版) 多項式回帰 一般線形モデル
一般化線形モデル 離散選択(英語版) ロジスティック回帰 多項ロジット(英語版) 混合ロジット(英語版) プロビット(英語版) 多項プロビット(英語版) 順序ロジット(英語版) 順序プロビット(英語版) ポアソン(英語版)
多水準モデル(英語版) 固定効果(英語版) 変量効果 混合モデル
非線形回帰 ノンパラメトリック(英語版) セミパラメトリック(英語版) ロバスト(英語版) 分位点(英語版) 等調(英語版) 主成分(英語版) 最小角度(英語版) 局所 折れ線(英語版)
変数誤差(英語版)
推定
最小二乗法 線形(英語版) 非線形
普通(英語版) 加重(英語版) 一般化(英語版)
部分 総最小二乗法(英語版) 非負(英語版) リッジ回帰 正則化(英語版)
最小絶対偏差(英語版) 繰返し加重(英語版) ベイズ(英語版) ベイズ多変量(英語版)
背景
回帰検証(英語版) 平均応答と予測応答(英語版) 誤差と残差 適合度(英語版) スチューデント化残差 ガウス=マルコフの定理
表話編歴
回帰(、英: regression)とは、統計学において、Y が連続値の時にデータに Y = f(X) というモデル(「定量的な関係の構造[1]」)を当てはめること。
別の言い方では、連続尺度の従属変数(目的変数)Y と独立変数(説明変数)X の間にモデルを当てはめること。X が1次元ならば単回帰、X が2次元以上ならば重回帰と言う。Y が離散の場合は分類と言う。
回帰分析(、英: regression analysis)とは、回帰により分析すること。
回帰で使われる、最も基本的なモデルは Y = A X + B {\displaystyle Y=AX+B} という形式の線形回帰である。
歴史
「回帰」という用語は、英語の「regression」からの翻訳であるが、元々は生物学的現象を表すために19世紀にフランシス・ゴルトンによって造られた。
ゴルトンは、背の高い祖先の子孫の身長が必ずしも遺伝せず、先祖返りのように平均値に戻っていく、すなわち「逆戻り、後戻り(=regression)」する傾向があることを発見した。これを「平均への回帰」という。
ゴルトンはこの事象を分析するために「線形回帰(英: linear regression)」を発明した。
ゴルトンにとって回帰はこの生物学的意味しか持っていなかったが、のちに統計学の基礎となり、「回帰(英: regression)」という用語も統計学へ受け継がれたのである。
概要
回帰分析では独立変数と従属変数の間の関係を表す式を統計的手法によって推計する。
従属変数(目的変数)とは、説明したい変数(注目している変数)を指す。
独立変数(説明変数)とは、これを説明するために用いられる変数のことである。
経済学の例を挙げてみると次のようになる。
経済全体の消費( Y {\displaystyle Y})を国民所得( X {\displaystyle X})で説明する
消費関数が Y = a X + b {\displaystyle Y=aX+b} というモデルで表されるとする。
この例では、消費 Y が従属変数、国民所得 X が独立変数に対応する。
そして a {\displaystyle a}、 b {\displaystyle b} といった係数(パラメータ)を推定する。
最も単純な方法は上式のような一般化線形モデルを用いる線形回帰であるが、その他の非線形モデルを用いる非線形回帰もある。
モデル
線形(一般化線形モデル、一般線形モデルなど)
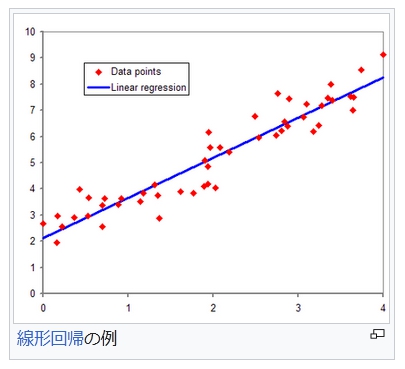
線形回帰の例
線形回帰
正則化項付き
リッジ回帰
ラッソ回帰
エラスティックネット
非線形
k近傍法
回帰木
ランダムフォレスト
ニューラルネットワーク
サポートベクター回帰
射影追跡回帰
多変量適応的回帰スプライン(英語版)
最小二乗法による推定
詳細は「最小二乗法」を参照
パラメータを推定する代表的な方法として、最小二乗法がある。これは、二乗和誤差を最小化する最尤推定である。
最小二乗法の概要は次の通りである。
初めに回帰式(目的変数を説明変数で計算する式)を設定する。
次に、回帰式の係数を求めるが、「従属変数の測定値と、独立変数の測定値および回帰式を用いて求めた推定値の差の二乗和誤差」が最小になるように求める。
線形モデルの場合、回帰式の係数で推定値の差の2乗平均を微分し0と置いた連立方程式を解いて求められる。
独立変数同士の相関
マーケティングやアンケートでよく使う一般的な重回帰の場合、複数の説明変数同士は強い相関がないという仮定が入っている。
そのため、一般化線形モデルで説明変数同士が関連性の高いものを使うと係数が妙な値になることがあるので注意する必要がある(これは多重共線性と呼ばれる)。
例:小学校での定期テスト得点から重回帰で分析する場合に、理科の点数を従属変数に、算数と国語を説明変数にした場合、算数が増えると理科の点数が多く、国語の点数が高ければ理科の点数が減るといった意味の係数が出ることがある。
これは算数と国語の点数に強い相関が両者にあるからである。
この場合は算数と国語の平均点と、算数と国語の得点の差というように和と差に数字を加工すると、この2つは相関が大抵低く、かつ解釈しやすい。
算数と国語の得点の差は、算数の方が高い生徒の方が理科の点数が高い傾向があるというように理解できるからである。
これは、線形モデルの問題であるため、線形モデルが不適切ならば、非線形モデルを使用すればよい。また、共分散構造分析という重回帰より複雑な関係を適切に説明できるモデルもある。
語源
回帰は語源的には回帰効果(平均への回帰)に由来する。回帰効果は相関(直線的な関係)が低い場合に顕著に現れる。しかし回帰分析では必ずしも直線的関係を仮定しない。また「目的変数yを説明変数xに回帰する」といい、「回帰」という言葉が由来とは異なる意味に使われている。
解析ソフト
NAG
IMSL
R言語 - 統計解析言語。回帰分析ほか多くの統計関数を標準装備したフリーウェア。『モデル式』でモデル記述や当てはめが容易。他アプリケーションのファイル取込やODBC接続対応。FDA公認。CRANという仕組みで世界の膨大なソフトを無償利用可能。可視化機能に優れ、日本語対応。マルチプラットフォーム。
Stata
Gretl
脚注
^ 『統計学入門』(東京大学出版会)、257頁
参考文献
『統計学入門』東京大学出版会、1991年。
J. R. Taylor 著、林茂雄、馬場凉(訳) 編『計測における誤差解析入門』東京化学同人、2000年。
蓑谷千凰彦『回帰分析のはなし』東京図書、1985年。
関連項目
統計学
計量経済学
相関係数
傾向推定
曲線あてはめ
アンスコムの例
分散拡大係数
多重共線性
表話編歴
統計学
標本調査
標本 母集団 無作為抽出 層化抽出法
要約統計量
連続確率分布
位置
平均
算術 幾何 調和 中央値
分位数 順序統計量 最頻値 階級値
分散
範囲 偏差 偏差値 標準偏差 標準誤差 変動係数 決定係数 相関係数 自己相関 共分散 自己共分散 分散共分散行列 百分率 統計的ばらつき
モーメント
分散 歪度 尖度
カテゴリデータ
頻度 分割表
推計統計学
仮説検定
パラメトリック
t検定 ウェルチのt検定 F検定 Z検定 二項検定 ジャック-ベラ検定 シャピロ–ウィルク検定 分散分析 共分散分析
ノンパラメトリック
ウィルコクソンの符号順位検定 マン・ホイットニーのU検定 カイ二乗検定 イェイツのカイ二乗検定 累積カイ二乗検定 フィッシャーの正確確率検定 尤度比検定 G検定 アンダーソン–ダーリング検定 コルモゴロフ–スミルノフ検定 カイパー検定 マンテル検定 コクラン・マンテル・ヘンツェルの統計量
その他
帰無仮説 対立仮説 有意 棄却
区間推定
信頼区間 予測区間
モデル選択基準
AIC BIC WAIC MDL
その他
偏り 偏りと分散 過剰適合 推定量 点推定 最尤推定 尤度関数 尤度方程式 最小距離推定 メタアナリシス ブートストラップ法
ベイズ統計学
確率
主観確率 ベイズ確率 事前確率 事後確率 最大事後確率
その他
ベイズ推定 ベイズ因子
相関
交絡 ピアソンの積率相関係数 順位相関(スピアマンの順位相関係数 ・ケンドールの順位相関係数 )
モデル
一般線形モデル 一般化線形モデル 混合モデル 一般化線形混合モデル
回帰
線形
リッジ回帰 ラッソ回帰 エラスティックネット
非線形
k近傍法 決定木 ランダムフォレスト ニューラルネットワーク サポートベクターマシン 射影追跡回帰
時系列
自己回帰モデル 自己回帰移動平均モデル ARCHモデル 対移動平均比率法 トレンド定常 傾向推定 共和分 構造変化
分類
線形
線形判別分析 ロジスティック回帰 <! -- 名前に回帰とついていますが確率を回帰する分類手法です --> 単純ベイズ分類器 単純パーセプトロン 線形サポートベクターマシン
二次
二次判別分析
非線形
k近傍法 決定木 ランダムフォレスト ニューラルネットワーク サポートベクターマシン ベイジアンネットワーク 隠れマルコフモデル
その他
二項分類 多クラス分類 第一種過誤と第二種過誤
教師なし学習
クラスタリング
k平均法 (k-means++法 ) DBSCAN
密度推定(英語版)
カーネル密度推定 ( カーネル )
その他
主成分分析 独立成分分析 自己組織化写像
統計図表
棒グラフ バイプロット(英語版) 箱ひげ図 管理図 フォレストプロット ヒストグラム 円グラフ Q-Qプロット ランチャート 散布図 幹葉表示 バイオリン図 ドットプロット ヒートマップ 階級区分図
生存分析
生存関数 カプラン=マイヤー推定量 ログランク検定 故障率 比例ハザードモデル
歴史
統計学の創始者 確率論と統計学の歩み
応用
社会統計学 疫学 生物統計学 系統学 統計力学 計量経済学 機械学習 実験計画法
出版物
統計学に関する学術誌一覧 重要な出版物
全般
統計 頻度主義統計学 統計学および機械学習の評価指標
その他
方向統計学 S言語 R言語 統計検定 社会調査士 JDLA Deep Learning For GENERAL JDLA Deep Learning for ENGINEER 実用数学技能検定 品質管理検定
カテゴリ カテゴリ
典拠管理データベース: 国立図書館 ウィキデータを編集
フランス BnF data ドイツ イスラエル アメリカ 日本 チェコ
カテゴリ:
統計学計量経済学数学に関する記事分析
最終更新 2023年10月19日 (木) 07:58 (日時は個人設定で未設定ならばUTC)。
テキストはクリエイティブ・コモンズ 表示-継承ライセンスのもとで利用できます。追加の条件が適用される場合があります。詳細については利用規約を参照してください。
』