ベルヌーイ分布

ベルヌーイ分布
https://ja.wikipedia.org/wiki/%E3%83%99%E3%83%AB%E3%83%8C%E3%83%BC%E3%82%A4%E5%88%86%E5%B8%83

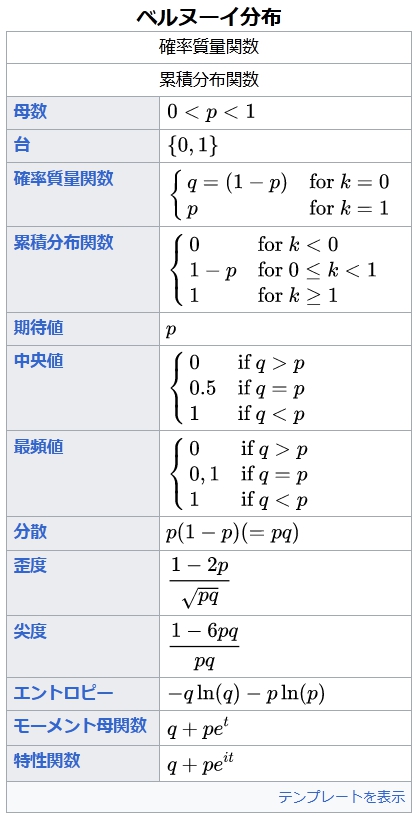
『出典: フリー百科事典『ウィキペディア（Wikipedia）』

ベルヌーイ分布
確率質量関数
累積分布関数
母数 0 < p < 1 {\displaystyle 0 p 0.5 if q = p 1 if q < p {\displaystyle {\begin{cases}0&{\text{if }}q>p\0.5&{\text{if }}q=p\1&{\text{if }}q p 0 , 1 if q = p 1 if q < p {\displaystyle {\begin{cases}0&{\text{if }}q>p\0,1&{\text{if }}q=p\1&{\text{if }}q<p\end{cases}}}
分散 p ( 1 − p ) ( = p q ) {\displaystyle p(1-p)(=pq)}
歪度 1 − 2 p p q {\displaystyle {\frac {1-2p}{\sqrt {pq}}}}
尖度 1 − 6 p q p q {\displaystyle {\frac {1-6pq}{pq}}}
エントロピー − q ln ⁡ ( q ) − p ln ⁡ ( p ) {\displaystyle -q\ln(q)-p\ln(p)}
モーメント母関数 q + p e t {\displaystyle q+pe^{t}}
特性関数 q + p e i t {\displaystyle q+pe^{it}}
テンプレートを表示

ベルヌーイ分布（英: Bernoulli distribution）とは、数学において、確率 p で 1 を、確率 q = 1 − p で 0 をとる、離散確率分布である。

ベルヌーイ分布という名前は、スイスの科学者ヤコブ・ベルヌーイに因んでつけられた名前である。

X をベルヌーイ分布に従う確率変数とすれば、確率質量関数は

P ( X = 1 ) = p , P ( X = 0 ) = q = 1 − p {\displaystyle P(X=1)=p,\qquad P(X=0)=q=1-p}

である。これを

P ( X = k ) = p k ( 1 − p ) 1 − k ( k = 0 , 1 ) {\displaystyle P(X=k)=p^{k}(1-p)^{1-k}\qquad (k=0,1)}

と一括することもできる。確率変数 X の平均は p, 分散は pq = p(1 − p) である。ベルヌーイ分布は指数型分布族の一つである。

ベルヌーイ分布

共有: