落ちないばねの不思議

国際物理オリンピック過去問シリーズルES公ハ
————————————- 物理教育は今
落ちないばねの不思議——国際物理オリンピック2019の理論問題

落ちないばねの不思議――国際物理オリンピック2019の理論問題 (jst.go.jp)

東辻浩夫f (totsiyi-09@t.okadai.jp)

はじめに

物理オリンピック日本委員会の活動に参加して約9年で
あり,国際物理オリンピック(IPh〇)への日本代表派遣に
オブザーバーとして随行したのは2019年イスラエル大会
が初めてである.したがってIPhOの現場によく通じてい
るわけではないが,代表を選ぶ過程である「第1,第2物
理チャレンジ」の,後者にかかわってきた経験も踏まえて,
感じるところを述べたい.

取り上げるのは2019年の理論第1問の力学である.第2
問はマグネトロン,第3問は熱・音響エンジンで,力学,
電磁気,熱の分野構成は標準的である.°解答時間は5時
間,配点は各10点満点であるが,第1問,第2問,第3問
の順に難しかった.

また,当然ながら力学分野は毎年出題
されているが,例年に比べてもやや難しかったと思われる.

スリンキー(ゼロ長ばね)の釣り合いと落下

「ばね」は高校における力学で弾性カと波動の項目に必
ず登場する.前者では,ばねの長さが］で自然長が”の
とき,張力Fは伸びx = L~L.に比例係数(ばね定数)kで
比例し,
F = kx = kL〇– (1)
L〇
と表されると説明される.また,後者の縦波の説明で,上
式はx<0のときも含むことが分かる.重力加速度の大きさ
がgのとき,質量mを「軽い」ばねに吊り下げると,kx = mg
で釣り合い,伸びはx = mg/kとなる.

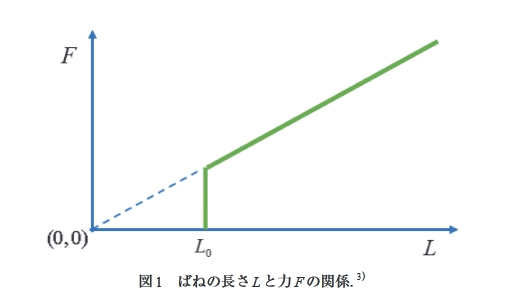
この問題では,はじめに,Fと］の次の関係が図1で示
される.
F = kL (£>Z〇) (2)
これは,式(1)でを〇としたものにあたり,「スリンキー」
「公益社団法人物理オリンピック日本委員会,岡山大学名誉教授
あるいは「ゼロ長ばね」と呼ばれる,という説明がある.

スリンキーはIPhOレベルの問題集では,しばしば題材と
なっている.ガ以下ではスリンキーを単にばねと呼ぶ.

問題はA, B, Cに分かれている.解いてみる方もおられ
ると思うので,まず,問いの要点を()内の配点ととも
にまとめて示す(実際の問題•解答はJPhOのホームペー
ジなどにある3)).

質量Mの一様なばねの各部を自然長のときの端からの
距離£(〇<£<“)で表し,£ = 0が吊り下げた時の下端にな
るとする.また,パラメータa = kLjMg(く’)を定義する.

静力学
A.1(0.5)自然の状態で長さ△£の微小部分の,ばねが
外力ドで引き伸ばされたときの長さ△マは?
A.2(0.5)△£を△マまで伸ばすのに必要な仕事△匠は?
A.3(2.0)このばねを吊り下げたときの全長Hをん〇と
αで表せ.
続いて,A.3の吊り下げた状態から上端を切り離したと
きの運動について,図2を示して説明してある.切り離す
と上から徐々に落ちていき,ばねの上部には自然長に戻っ
たかたまりが生じる.かたまりの長さは徐々に伸びるが,
その下の部分は静止したままである.下端は全部がかたま
りになってから動き出す.

図2
左:スリンキーの自由落下中に撮影した連続写真.右:ばねの自由
落下中の移動する部分(part I)および静止している部分(part 11).3)
物理教育は今落ちないばねの不思議
637
©2020日本物理学会

動力学
B.l(2.5)自然の長さ”に戻るまでの時間ん(およびそ
の数値)は? {k=1.02 N/m, L〇 = 0.055 m, M= 0.201 kg,
g = 9.80 m/s2)
B.2(2.5)静止したままの部分の質量が(£/”) Mのと
き,動いている部分の速さの(のがの(の=M+3で
あることを示し,定数れ8を£〇, g, αで表せ.
B.3(0.5)B.2に基づいて,動いている部分の速さの最
小値”minを求め,L〇, a, A, 8で表せ.

問題の最後は,

エネルギー論
C (1.5)放してから地上に達する直前までに熱となる
力学的エネルギー Qを求め,L〇, M, g, αで表せ.
Aでは自重で吊り下げた状態について問う.A.1で,微
小部分△£について張力と長さの関係を問い,それをもと
に,A.2, A.3で蓄えられるエネルギーと全長を求めさせて
いる.ばねが変形する様子を想像すれば,ばねの張力が元
の長さとの比に比例することに気付くであろう.A.2では,
(△ソー察)2に比例した解答は〇点とするよう採点要領
(marking scheme)で指示されており,図1の正確な理解を
求めている.F(£ + A^) -F(€)を△£で表し,質量が一様分
布していることから次の式を得る.

dF(C) _ M

A.3では,張力ドは各部分で異なり,F<kし〇すなわち
ev〇し〇では,ばねは変形しない(伸びない)ことに注意す
る必要がある.このことはBで図2をよく見れば気付く.
ばねの微小部分に着目するよう誘導しており,前提とは
していないが,局所的な張力の満たす微分方程式の想定を
暗黙に要求しているともいえる.これはIPhOなどの問題
の一つの特徴である.日本の教科書では,巻末に「発展」
として,「微分•積分を使った物理」のような表題で説明
されている,簡単な常微分方程式に基づく扱いに相当する.
第2物理チャレンジの理論の作問でも,テーマの選択や難
易度とともに議論になることがあるが,教科書の「発展」
にあるような簡単な常微分方程式の誘導は許容されると考
えている.4)

Bで問われているのは,一見,複雑な運動であるが,ば
ねに働くタ、カは重力だけであるから,ばねの重心に着目す
ると自由落下である.このことに気が付けば,図2につい
ての説明から重心の位置が求まり,解が得られる.出題の
意図は重心が自由落下することに気付くかを問いたい,で
あると思いたい.しかし,ここでも,ばねの各部の高さが
与えられたとき,重心(モーメント)を求める積分が必要
になる.また,積分は単純だが,の(のと重心の速度の違
638

答えの
関数形を与えたのはそれを考慮したためかと思われる.

一方,B.3では,伸びないままであった〇3<aし〇の部分と
合体して,全長が”に戻った直後が最小であるが,合体
する直前を答える不注意が誘われそうである.

上端を切り離しても,切り離したという信号がまだ伝
わってこない部分はそのままで,落ちない.このような動
画を掲載しているサイトもあるので,グ見慣れている参加
者もいたかもしれないが,多くは「これは面白そうだ」と
思ったのではないか.

最後に,Cでエネルギー保存について問う.外力の仕事
は自然長にもどったばねの運動エネルギーになるが,A.2
で問うたばねに蓄えられたエネルギーが保存されない.
全体を通じて,物理は単純で面白い.しかし,計算は間
違えやすい.パラメータαが含まれた答えが出ても正しい
かどうかを形からは判断しにくいので,慎重に確かめる必
要がある.IPhOでは,そのような判断ができるような問
題では差がつきにくいのだろう.

それぞれの設問の解答は次のとおりである.

A.1(0.5)
Ay =—A£(F > kL〇), Ay = A€(F < kL〇)
紅0
A.2(0.5)
心=地(△ソ2ー破)
A. 3 (2.0)
TY
B. l (2.5)
tc= I— (1-a)3 =0.245 s
\I 3ga
B.2(2.5)
A =丑,B = -lLz〇
3a Ua K
B.3(0.5)
〇min =(1 – a) +3
C (1.5)
〇=以卯。(1ーげ⑵+1)
6a

3.普通のばねではどうなるか

この問題では,はじめからゼロ長ばねとしている.この
ため,吊り下げたとき,最下部に伸びない部分が生じ,釣
り合いを少し複雑にしている.では,普通のばねではどう
なるであろうか.釈迦に説法だが,スリンキーとの比較の
ため敢えて示す.

一様な伸びのとき,ばねの張力と長さの関係は式(1)で
あるから,点£ =”で吊り下げると,微小部分△£の長さと
日本物理学会誌 Vol. 75, No.10, 2020
全長は次のようになる.

全体の伸びは”/2aで,同じばね定数をもつ軽いばねの端
に質量Mを吊り下げたときの1/2である.
さて,このばねを上端€ = £〇で切り離したらどういう運
動をするであろうか.各部分の上方への変位を”(£”),
i<〇 (€) = u (ん0)とすると
1 夕2
(。 <£<ん〇).
し〇 2a
運動方程式は
M )”(£,/) _ d2u(£, /) _ 1
kL0 dt2 ° df a
となり,u = Ul~gt2/2とおくと,肉(5 は斉次の波動方程
式を満たす.
/ = 0に上端を切り放すと,上下端は自由端となる.“〇(£)
を-Z〇<£<£〇に用い,その外では周期2″の周期関数
(“〇(£ +2”) =“〇(£))として定義域を拡張すれば,運動方
程式の解は,c=(k”%として,次のようになる.
u(£, i) = — g」+ & 3〇(£ — ci) + “〇(£ + ct)］
0 く ctくL〇 — e では,
u U, t) = — + —-— (£2 + c2/2) =-= “〇(•£)
2 2aL0 2aL0
となり,上端を切り離しても,0<c/=［(“ルが勺:〇レ<
(“-£)であれば落ちない.ばねの各部分には重力と上下
からの張力が作用しているが,切り離したという信号が速
さ&”細でばねを経由して上端(, = “)から伝わるま
では張力は変化せず,釣り合ったままである.
一方,0<” —£<cM〇では,
m)=二一“”此
2aL〇 a
duU, t) _ し〇~£
–:–_—< u
dl aL〇
で,(£ = “を除いて)ばねは縮んでいる.

教科書の波動の項目では,弦巻ばねの一方の端をある瞬
間に押したり引いたりすると,その端から疎密波が伝わっ
ていく様子の図が出ている.同じことであるが,上端を切
り離してからしばらくは動かない(落ちない)ことを見れ
ば,媒質が近接作用によって力を伝えるときの速度が有限
であることの効果をより実感できるであろう.釣り合いで
の伸びの形や運動方程式やその解は知らなくても,落ち始
めるまでの時間はばねの振動が伝わる速度だけで決まるの
で,現在の高校教科書の範囲でも問うことができると思わ
れる(教養課程の物理履修者には具体的に解いてほしい).

このIPhOの問題では落下するときの振る舞いを図2で
説明している.一見,不思議であるが,普通のばねでも同
じような現象があるから,後者を考えたことがあれば納得
できると思われる.し

4.スリンキーの方が簡単?

この問題の重要な要素は,ばねにスリンキーを使ったこ
とである.この場合を”⑸と表すと,問題A.1のように,
張力と伸びの関係は式(2)から

kL〇血ジ⑵=F(e) — kL〇, (F > kL〇),
血如)= °, (F く kL〇)
d£
であるから
“貞の=¢了〇)2 , 0 <(“乙〇 —a)<(l —α)
2aL〇
—。 , — a< 或|Lq — a) < 0
となる.

このように,0<£/”<aではばねは伸びない.こ
れが,釣り合い時のスリンキー効果である.
—+ gt2/2に対する運動方程式は同じ形であるが,解は
次を満たす必要がある.

(力・)> 0 (3)
d£ ～

これが運動時のスリンキー効果である.
上端(€ = !〇)の境界条件は普通のばねのときと同じく自
由境界条件である.また,C = aL〇では(初双)措あ(£)= 0で
あるから,M〇 =1とM〇-ct = 0を自由境界と考えれば,
113)を|加0-al<(l-α)に用い,その外には周期
2(1-α)”の周期関数として”rの定義域を広げて,解は
次で与えられそうである.

“⑸(£, i)=—,ヽ + ［購)以一赤)+ 我)(£ + ct)］
確かに,aL〇<£<L〇-ctでは,次のようにばねは落ちない.
が幻¢,)= ー妃+ °ー”。)2 +(づ2 =借)(の
しかし,aL〇<L〇-ct<£<L〇では,
林t)=『毒ユ<ルいL。), 2aL〇 a “)(£,‘) L〇-£
——_—-< 0
d£ aL〇
となる.舟S)はe=L0-ctで”⑸(£,」= 〇)と連続してい
るカキ£ = Lo以外では式(3)を満たさず,•とともに式(3)
の左辺が負の部分は上端から広がる.このように,この
M(S)« i)はスリンキーの場合の解になっていない.このこ
とは普通のばねの場合に〇くで縮んでいたことか
ら明らかである.

IPhOの設問では,上端から(&双)”⑸(£”)= 〇の領域が
広がるとして,広がる速さを問うている.収縮した部分が
広がるのは一種の衝撃波であるが,重心の自由落下から設
問のようにうまく運動が解ける.考えている系における外
カと内力の作用の違いに着目するのは常套手段とも言える
物理教育は今落ちないばねの不思議
639
©2020日本物理学会
が,IPhOに参加した代表に限らず学んでほしい.

この問題では,スリンキーは(引双)”⑸¢か=〇になる
と瞬時に収縮する,と仮定する簡単なモデルに基づいた解
析に誘導している.その仮定を緩めると,実際のスリン
キーの落下のデータとより合うモデルになる,という解析
もある.7)

波動方程式を正面からもちだすのはIPhOのシラバス8)
との関係が微妙である.したがって普通のばねの落下をそ
のまま問うことは難しいかもしれない.

一方,スリンキー
の場合は普通のばねと同じ扱いでは解がうまく求まらない
が,適切に誘導すれば初等的な方法で解ける.そこで後者
を問題にしたが,本当は波動方程式で記述される現象を出
題したかったのかもしれない.

5•おわりに

この力学の問題は他の分野の問題に比べて難しく,1/2
程度得点できた代表もいたが,平均的に得点はあまり高く
なく,特にBが難しかった.

これは他の多くの国の代表も
同じであると思われる.

また,第1問であり,問題の面白
さもあるので,他の比較的易しい問題への時間配分ができ
にくかったようである.

この問題の中心はBであり,そのような配点となってい
る.

Bで求められていることは,物理としては,この系に
働くタ!・力が何かと,それによる運動を把握することである
が,解を求めるには,重心の移動を具体的に求めなければ
ならない.

採点要領では,物理的な考察に比べて後者の配
点が大きめであり,工夫できないかと感じる.

IPhOのシラバスでは,解析(Calculus)の項では常微分
方程式に言及していないが,力学(Statics, Dynamics)の項
で重心や慣性モーメントを積分で求めることを含んでい
る.

砂例えば,局所的な変位(伸び)から全体の変位を求
めるのは,単なる積分ともいえるが,この問題を解く上で
は必須である.

物理オリンピックに関係する場面に限らず,一般に,物
理現象を積極的に使い,物理と微分•積分の両方の理解を
深めるのにもっと役立てたらどうかと感じている.

微分・
積分の履修者には,適切な具体例として役立つであろうし,
物理の例から出発して微分•積分を教えることもできるの
ではないか.

物理を履修する生徒も,おもちゃとしてスリンキーを目
にした,あるいは触ってみたことがあると期待する.また,
普通のばねは誰でも知っている.

しかし,理系の教育を受
けた社会人でも,パズルとして,弦巻ばねを自重で吊り下
げ,手を離したらどうなるかを聞いてみると,手を離した
瞬間に下端も落下を始めると思う人も多いようである.

こ
のようなありふれた素材の,ちょっと意外な振る舞いに気
付かせ,それが,力学の簡単な原理で求まることを示して
いる点で,面白い問題である.

高校生や中学生に,物理(あるいは理科一般)に興味を
もってもらうためには様々な方策が考えられる.

ノーベル
賞などの報道で注目される現象や原理を取り上げるのもー
つである.

一方で,身近な現象や素材を用いて,物理(理科)
的な考察により「なるほど」と思わせるのも一つの方法で
ある.

IPhOの問題にも,身近に経験できる現象で,一見不
思議だが,細かい計算はすぐには追えないにしても,こう
考えれば理解できそうだ,というようなものがあってよい.

参考文献
1) 実験を含む他の問題の紹介は,杉山忠男,日本物理学会誌75, 355
(2020)にある.
2) 例えば,P. Gnadig, G. Honyek, and M. Vigh, 200 More Puzzling Physics
Problems with Hints and Solutions (Cambridge Univ. Press, Cambridge,
2016);伊藤郁夫監訳,赤間啓一,他訳,『もっと楽しめる物理問題
200 選 Part 1,11』(朝倉書店,2020).
3) 和訳は http://www.jpho.jp/ipho.html U,元の英文は https://www.ipho2019.
org. il/problems-solutions/ にある.
4) 物理チャレンジでは,中学理科から高校物理の範囲を基本とし,その
範囲を超える問題には解説やヒント,誘導をつけて出題される(http://
http://www.jpho.jp/junbi.html),問題例は JPhO ホームページ(http://www.jpho.
jp/syllabus.html)にある.例えば,2019年第2チャレンジの理論問題(解
答時間は5時間)の各問の表題は,第1問テニス壁打ち,第2問流体の
流れと砂の流れ,第3問電気回路,第4問電磁波と重力波・
5) 例えば,「スリンキーの落下」,「落ちないばね」,”Slinky Fall (Drop)”
などで検索すると多数の動画が見つかる.
6) 普通のばねの場合の例に,https://www.youtube.com/watch?v=8NP-
NB7kW-I (Spring Fall/バネで繋がれた粒子の落下運動)がある.
7) この問題で誘導している解法は,例えば,M. G. Calkin, Am. J. Phys.
61,261(1993).仮定を緩めた解は,例えば,R. C. Cross and M. S.
Wheatland, Am. J. Phys. 80,1051(2012),およびそれらに引用されてい
る文献・
8) https://www.ipho-new.org/statutes-syllabus/
(2020年5月4日原稿受付)
日本物理学会誌 Vol.75, No.10, 2020
640
©2020日本物理学会

落ちないばねの不思議

共有: