複素数の歴史
https://ja.wikipedia.org/wiki/%E8%A4%87%E7%B4%A0%E6%95%B0

　※　今日は、こんな所で…。

　※　上記より、「歴史」の部分だけ抜粋した。

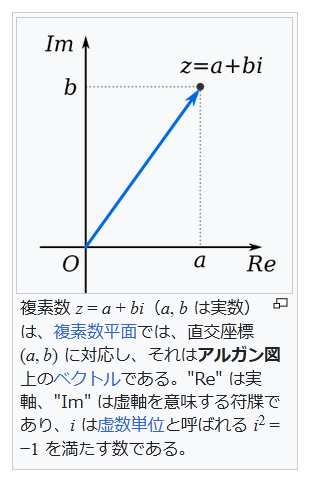
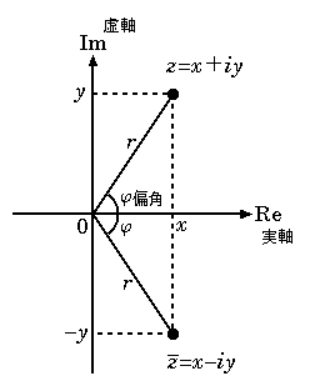
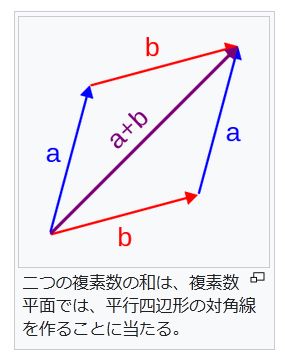
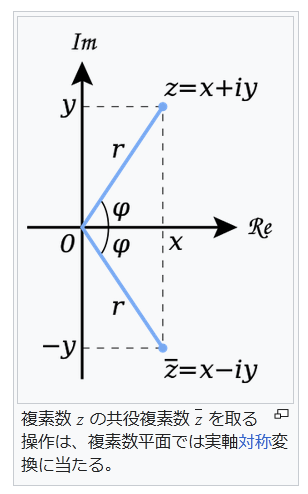
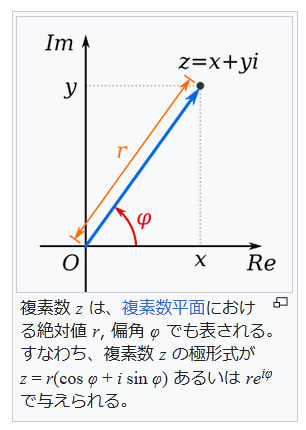
『歴史

負の数の平方根について、いささかなりとも言及している最も古い文献は、数学者で発明家のアレクサンドリアのヘロンによる『測量術』(Stereometrica) である。そこで彼は、現実には不可能なピラミッドの錐台について考察しているものの、計算を誤り、不可能であることを見逃している。

16世紀にイタリアの数学者カルダノやボンベリによって三次方程式の解の公式が考察され、特に相異なる 3 個の実数解を持つ場合に解の公式を用いると、負の数の平方根を取ることが必要になることが分かった。

当時は、まだ、負の数でさえあまり認められておらず、回避しようと努力したが、それは不可能なことであった。

17世紀になりルネ・デカルトによって、虚 (imaginary) という言葉が用いられ、虚数と呼ばれるようになった。

デカルトは作図の不可能性と結び付けて論じ、虚数に対して否定的な見方を強くさせた。
その後、ウォリスにより幾何学的な解釈が試みられ、ヨハン・ベルヌーイやオイラー、ダランベールらにより、虚数を用いた解析学、物理学に関する研究が多くなされた。

複素平面が世に出たのは、1797年にノルウェーの数学者カスパー・ベッセル（英語版） (Caspar Wessel) によって提出された論文が最初とされている。

しかしこの論文はデンマーク語で書かれ、デンマーク以外では読まれずに1895年に発見されるまで日の目を見ることはなかった。

1806年にジャン＝ロベール・アルガン（英語版） (Jean-Robert Argand) によって出版された複素平面に関するパンフレットは、ルジャンドルを通して広まったものの、その後、特に進展は無く忘れられていった。

1814年にコーシーが複素関数論を始め、複素数を変数に取る解析関数や複素積分が論じられるようになった[15]。

1831年に、機は熟したと見たガウスが、複素平面を論じ、複素平面はガウス平面として知られるようになった[16]。

ここに、虚数に対する否定的な視点は完全に取り除かれ、複素数が受け入れられていくようになる。

実は、ガウスはベッセル（1797年）より前の1796年以前にすでに複素平面の考えに到達していた。1799年に提出されたガウスの学位論文は、今日、代数学の基本定理と呼ばれる定理の証明であり[17]、複素数の重要な特徴付けを行うものだが、複素数の概念を表に出さずに巧妙に隠して論じている[16]。

他分野における複素数の利用

複素数 A と実数 ω により定まる、一変数 t の関数 Aeiωt は時間 t に対して周期的に変化する量を表していると見なすことができる。

周期的に変化し、ある種の微分方程式を満たすような量を示すこのような表示はフェーザ表示と呼ばれ、電気・電子工学における回路解析や、機械工学・ロボット工学における制御理論、土木・建築系における振動解析で用いられている[18]。

物理学

物理における振動や波動など、互いに関係の深い2つの実数の物理量を複素数の形に組み合わせて表現すると便利な場面が多いため、よく用いられる。

量子力学では複素数が本質的である（数学的な定式化に用いられる）。

物体の位置と運動量とはフーリエ変換を介して同等の扱いがなされ、波動関数たちのなす複素ヒルベルト空間とその上の作用素たちが理論の枠組みを与える。

複素数の拡張

詳細は「多元数」を参照

複素数とは実数体上の、実数単位 1, 虚数単位 i の線形結合であるが、これに新たな単位を有限個加えて可換体（通常の四則演算ができる数の体系）を作ることはできない[19][20]。

実数体 R から拡張して C を得る過程はケーリー＝ディクソンの構成法と呼ばれる。

この過程を推し進めると、より高次元の四元数体 H, 八元数体 O が得られる。これらの、実数体上の線形空間としての次元はそれぞれ 4, 8 である。この文脈において複素数は「二元数」(binarions) とも呼ばれる[21]。

注意すべき点として、実数体にケーリー＝ディクソンの構成を施したことにより、順序に関する性質が失われていることである。

より高次元へ進めば実数や複素数に関してよく知られた性質が失われていくことになる。
四元数は唯一の非可換体であり[19][20]（つまり、ある二つの四元数 x, y に対して x·y ≠ y·x となる）、八元数では（非可換なばかりでなく）乗法に関する結合法則も失われる（つまり、ある八元数 x, y, z に対して (x⋅y)⋅z ≠ x⋅(y⋅z) となる）。

一般に、実数体 R 上のノルム多元体は、同型による違いを除いて、実数体 R, 複素数体 C, 四元数体 H, 八元数体 O の4種類しかない（フルヴィッツの定理（英語版））[22]。ケーリー＝ディクソン構成の次の段階で得られる十六元数環ではこの構造は無くなってしまう。

ケーリー＝ディクソン構成は、C（を R-線型環、つまり乗法を持つ R-線型空間と見て）の正則表現と近しい関係にある。すなわち、複素数 w に対して、R-線型写像 fw を

f w : C → C ; z ↦ w z {\displaystyle f_{w}:\mathbb {C} \to \mathbb {C} ;\;z\mapsto wz}

とすると、fw の（順序付き）基底 (1, i) に関する表現行列は、実二次正方行列

( Re ⁡ ( w ) − Im ⁡ ( w ) Im ⁡ ( w ) Re ⁡ ( w ) ) {\displaystyle {\begin{pmatrix}\operatorname {Re} (w)&-\operatorname {Im} (w)\\\operatorname {Im} (w)&\quad \operatorname {Re} (w)\end{pmatrix}}}

である（つまり、#行列表現で述べた行列に他ならない）。これは C の標準的な線型表現だが、唯一の表現ではない。実際、

J = ( p q r − p ) , ( p 2 + q r + 1 = 0 ) {\displaystyle J={\begin{pmatrix}p&q\\r&-p\end{pmatrix}},\quad (p^{2}+qr+1=0)}

なる形の任意の行列はその平方が単位行列の −1 倍、すなわち J2 = −I を満たすから、行列の集合

{ z = a I + b J : a , b ∈ R } {\displaystyle \{z=aI+bJ:a,b\in \mathbb {R} \}}

もまた C に同型となり、R2 上に別の複素構造を与える。これは線型複素構造（英語版）の概念によって一般化することができる。

超複素数は R, C, H, O もさらに一般化するもので、例えば分解型複素数環は剰余環 R[x]/(x2 − 1) である（複素数は剰余環 R[x]/(x2 + 1) であった）。この環において方程式 a2 = 1 は4つの解を持つ。

実数体 R は有理数体 Q の通常の絶対値による距離に関する完備化である。Q 上の別の距離函数をとれば、任意の素数 p に対して p 進数体 Qp が導かれる（つまりこれは実数体 R の類似対応物である）。オストロフスキーの定理によれば、この R と Qp 以外に Q の非自明な完備化は存在しない。Qp の代数的閉包 Qp にもノルムは伸びるが、C の場合と異なり、そのノルムに関して Qp は完備にならない。Qp の完備化 Cp は再び代数的閉体であり、C の類似対応物として p-進複素数体と呼ぶ。

体 R, Qp およびそれらの有限

次拡大体は、すべて局所体である。

（※　以下、省略。）』