【fortran】複素数の使い方

『2019年6月29日　2019年9月3日

概要
背景
実例

概要

fortranで複素数を使うには次のように宣言と代入をすれば良い。

COMPLEX a
a=(3.0,4.0) !(実部, 虚部)

背景

物理、天文学という古くからある分野に関わっていると、fortranが第一プログラミング言語という人も多い。

私もその中の一人で、社会に出てみると、まるで古典文学を書く人という扱いを同僚からうける。

しかし、fortranはまだ大活躍中の言語であり、スーパーコンピュータでの配列計算にはよく使われる言語である。

今回は虚数の使い方について記す。メモがわりに。

自然界に虚数は存在しない、少なくとも人間には観測できない。しかし我々は、その存在を許さない限り自然を説明できない。

実数を観測して、虚数を「見る」ことが多い。面白い。

実例

下記のコード例に複素数で重要な点を示した。

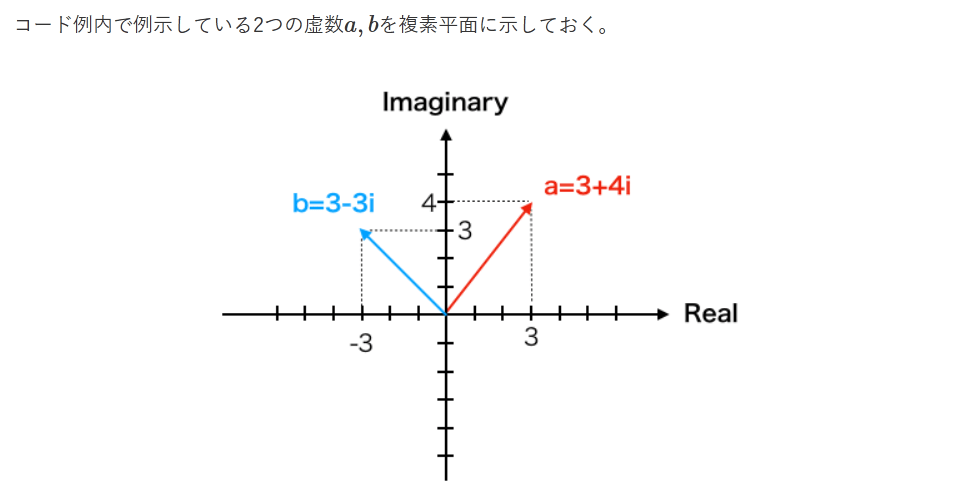
コード例内で例示している2つの虚数a,bを複素平面に示しておく。

imaginary

PROGRAM COMPLEX

IMPLICIT NONE !未宣言の変数を拒否するいつもの文言
COMPLEX a, b !複素数の変数としてa, bを宣言
REAL pi !円周率π用変数の宣言

pi=4.0*atan(1.0) !円周率をpiに代入。arctanを利用したこの書き方はよく使われる。

!複素数値の代入と、基本的な演算
a=(3.0,4.0) !複素数aを定義。a = 3 + 4i

PRINT *, ABS(a) !絶対値 -> 5.00000000

PRINT *, AIMAG(a) !虚部 -> 4.00000000

PRINT *, REAL(a) !実部 -> 3.00000000

!偏角の計算
b=(-3.0, 3.0)

PRINT , ATAN2(AIMAG(b), REAL(b))/pi180.0 !偏角 -> 135.000000

END PROGRAM COMPLEX

上記を実行すると、下記のような出力が得られる。

5.00000000
4.00000000
3.00000000
135.000000

このようにして、複素数の宣言と絶対値、虚部、実部の計算がされる。さらに、偏角の計算も示した。

一応偏角θの計算は下記に示しておく。

a=ar+aii⇒tan(θ)=aiar⇒θ=arctan(aiar)

もちろん、上記の式で得られるθはradで表されている。

上のコード上ではradから度に単位変換している。』