立方体倍積問題

立方体倍積問題
https://ja.wikipedia.org/wiki/%E7%AB%8B%E6%96%B9%E4%BD%93%E5%80%8D%E7%A9%8D%E5%95%8F%E9%A1%8C

『出典: フリー百科事典『ウィキペディア（Wikipedia）』

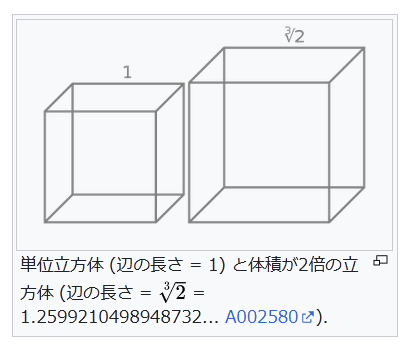
単位立方体 (辺の長さ = 1) と体積が2倍の立方体 (辺の長さ = 2 3 {\displaystyle {\sqrt[{3}]{2}}} = 1.2599210498948732… A002580).

立方体倍積問題（りっぽうたいばいせきもんだい）は、三大作図問題の1つである。古代エジプト人、ギリシア人、インド人にも知られていた[1]。

立方体倍積問題とは、一辺の長さがs、体積がV= s3のある立方体に対し、体積が2V、つまり一辺の長さが s ? 2 3 {\displaystyle s\cdot {\sqrt[{3}]{2}}}の立方体を与える問題である。この問題は、 2 3 {\displaystyle {\sqrt[{3}]{2}}} ? 1.25992105が作図可能数ではないため、定規とコンパスだけでは作図が不可能であることが証明されている[2]。

歴史

アポローンによってもたらされた疾病を鎮める方法を知るためにデルフォイの神託を求めたデロス島の市民の故事から[3]、「デロス島の問題」(Delian problem)とも呼ばれる。

プルタルコスによると[4]、島内の政治問題の解決法を探していたデロス市民が、デルフォイの神託を求めたとされている。

神託は、立方体の形状をしたアポローンの祭壇の大きさを2倍にせよと告げた。

デロス市民は、この答えを奇妙に感じ、プラトンに相談した。プラトンはこの神託を、与えられた立方体の体積を2倍する数学的問題と解釈し、アポローンがデロス市民に幾何学や数学を勉強させることで、その熱情を鎮めようとしていると説明した[5]。

プルタルコスによると、プラトンはエウドクソス、アルキタス、メナイクモスにこの問題を出題した。

メナイクモスは、機械的手段でこの問題を解いたが、プラトンから、純粋に数学的な方法で解決していないと非難された (Plut., Quaestiones convivales VIII.ii, 718ef)。

これが、紀元前350年代の『シシュポス』の中で、この問題が未解決問題として引用された原因かもしれない[6]。

この問題の解決の模索の大きな進歩は、キオスのヒポクラテス（英語版）が、この問題は、ある線分と2倍の長さの別の線分の2つの比例中項を求める問題と等価であると発見したことだった[7][8]。

近代風に言うと、長さaと2aの与えられた線分において、立方体の複製は次を満たす長さrとsの線分を見つけることと等価である。

a : r = r : s = s : 2 a .   {\displaystyle a:r=r:s=s:2a.\ }

解決

1837年に、ピエール・ヴァンツェルにより、2の立方根は作図可能数ではない、すなわち定規とコンパスによる作図は不可能であることが証明された[2]。

メナイクモスによる解法は、2つの円錐曲線の交点を用いるものだった。さらに複雑な解法としては、シッソイド、コンコイド、Philo lineを用いたものがある。

アルキタスは、紀元前4世紀に、回転体の3つの面の交点としてこの問題を解いた。

折り紙によっても、2の立方根を作ることができる。

脚注
[脚注の使い方]

^ Guilbeau, Lucye (1930). “The History of the Solution of the Cubic Equation”. Mathematics News Letter 5 (4): 8?12. doi:10.2307/3027812. JSTOR 3027812.
^ a b Wantzel, P M L (1837), “Recherches sur les moyens de reconnaitre si un probleme de Geometrie peut se resoudre avec la regle et le compas.”, Journal de Mathematiques Pures et Appliquees, 1 2: 366?372, EuDML 234865
^ L. Zhmud The origin of the history of science in classical antiquity, p.84, quoting Plutarch and Theon of Smyrna
^ Plutarch, De E apud Delphos 386.E.4
^ Plutarch, De genio Socratis 579.B
^ Carl Werner Muller, Die Kurzdialoge der Appendix Platonica, Munich: Wilhelm Fink, 1975, pp. 105-106
^ T.L. Heath A history of Greek mathematics, Vol. 1
^ Greek Mathematical Works, Volume I: Thales to Euclid. Translated by Ivor Thomas. Loeb Classical Library 335. Cambridge, MA: Harvard University Press, 1939. (Eutocius（アスカロンのエウトキオス）, Commentary on Archimedes' Sphere and Cylinder（アルキメデス『球と円柱について』註解） ii, Archim. ed. Heiberg iii. 88. 4-90. 13)

立方体倍積問題

共有: