折り紙による解

折り紙による解
http://www.takayaiwamoto.com/Greek_Math/Delian/ja_Origami_Delian.html

　※　解が、「実数解」の場合、必ずや「数直線」上に表現できるはずなんだ…。

　※　ただし、定規とコンパス使っては、実現できないことは証明済みらしい…。

　※　そこで、日本伝統の「折り紙」の登場だ…。

『1. 阿部恒の折り紙解 (ref.1)

阿部恒は1980年にユニークなデリアンの解を日本の学会誌「数学セミナー」に発表した。
その方法は、最近 2003年出版の
参考文献（ref.1）で述べられている。

彼は伝統的な日本の折り紙のテクニックを用いている。

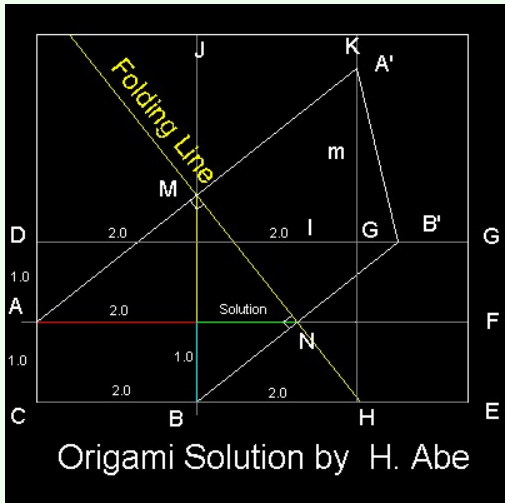
(1) 四角形の紙を用意する。四隅は全て正確に90度。
(2) 線分 AF, DG, BJ, HK は、折った跡の折り目線。
(3) 横線の間隔は1単位長さ。
(4) 縦線の間隔は二倍の単位長さ。
(5) 点H を要にして、点A が線HK上に、点Bが線DG上に
くるように紙を折る。

距離ON（緑の線）は2の立方根である。

ここをクリックしてアニメーションを見る。（　http://www.takayaiwamoto.com/Greek_Math/Delian/Abe_Delian_anim.gif　）

詳細は阿部恒の折り紙解の章で説明。
Origami_Delian_desc.dwg *

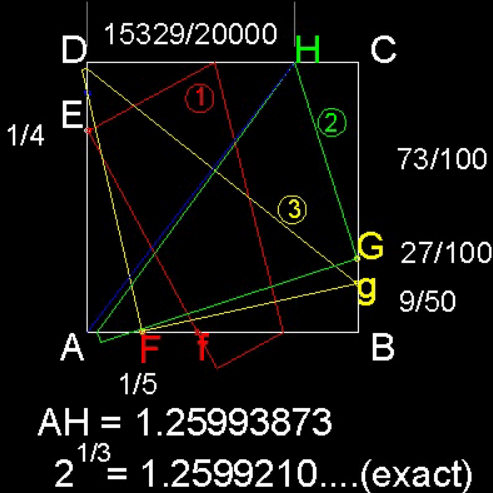
2.芳賀和夫の折り紙解 (ref.2)

Ref.2では正方形の紙で辺の長さ(15329/20000)の作り方を示している。

ABCD は正方形の紙。
ステップ 1: C が点E にくるように折る。辺CD は点f で線分AB と交差する。
Af を二分する点F を求める。
ステップ 2: C が点F にくるように折る。折り曲げ線は点g でCB と交差する。
Bg を50 %伸ばし、点G を定義する。
ステップ 3: D が点G にくるように折る。折り曲げ線は点H でCD と交差する。
長さ AH = 1.25993873 は 21/3 = 1.259921… にかなり近い近似値を得る。

ここをクリックしてアニメーションを見る。（　http://www.takayaiwamoto.com/Greek_Math/Delian/Haga_Delian_anim.gif　）

詳細は芳賀和夫の方法の章で説明。
Origami_Delian_2_desc.dwg *

参考文献

Abe, Hisashi: “Amazing Origami” , (in Japanese), 2003, ISBN 4-535-78409-4
Haga, Kazuo: “Origamics part – I” , (in Japanese), 1999, ISBN 4-535-78293-8 ホームページの内容目次に戻る古代ギリシャ数学の三大問題

質問、問い合わせは筆者岩本卓也宛てにお願いします。

Last Updated Nov 22, 2006

折り紙による解

共有: